
一透明的敞口正方體容器ABCD -A′B′C′D′ 裝有一些液體,棱AB始終在水平桌面上,容器底部的傾斜角為α (∠CBE = α,如圖1所示).
探究 如圖1,液面剛好過棱CD,并與棱BB′ 交于點Q,此時液體的形狀為直三棱柱,其三視圖及尺寸如
圖2所示.解決問題:
(1)CQ與BE的位置關系是 ,BQ的長是 dm;
(2)求液體的體積;(參考算法:直棱柱體積V液 = 底面積SBCQ×高AB)
(3)求α的度數.(注:sin49°=cos41°= ,tan37°=
,tan37°= )
)
拓展 在圖1的基礎上,以棱AB為軸將容器向左或向右旋轉,但不能使液體溢出,圖3或圖4是其正面示意圖.若液面與棱C′C或CB交于點P,設PC = x,BQ = y.分別就圖3和圖4求y與x的函數關系式,并寫出相應的α的范圍.
延伸 在圖4的基礎上,于容器底部正中間位置,嵌入一平行于側面的長方形隔板(厚度忽略不計),得到圖5,隔板高NM =" 1" dm,BM = CM,NM⊥BC.繼續向右緩慢旋轉,當α = 60°時,通過計算,判斷溢出容器的液體能否達到4 dm3.
(1)CQ∥BE, 3。
(2)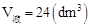 。
。
(3)37°。
拓展:y=-x+3. 37°≤α≤53°。
延伸:溢出液體可以達到4dm3
解析分析:探究:(1)根據水面與水平面平行可以得到CQ與BE平行,利用勾股定理即可求得BD的長: 。
。
(2)液體正好是一個以△BCQ是底面的直棱柱,據此即可求得液體的體積;。
(3)根據液體體積不變,據此即可列方程求解。
拓展:分容器向左旋轉和容器向右旋轉兩種情況討論。
延伸:當α=60°時,如圖6所示,設FN∥EB,GB′∥EB,過點G作GH⊥BB′于點H,此時容器內液體形成兩層液面,液體的形狀分別是以Rt△NFM和直角梯形MBB′G為底面的直棱柱,求得棱柱的體積,即可求得溢出的水的體積,據此即可作出判斷。
探究:(1)CQ∥BE, 3。
(2) 。
。
(3)在Rt△BCQ中,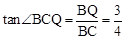 ,∴α=∠BCQ=37°。
,∴α=∠BCQ=37°。
拓展:當容器向左旋轉時,如圖3,0°≤α≤37°,
∵液體體積不變,∴ 。
。
∴y=-x+3.
當容器向右旋轉時,如圖,同理可得: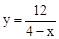 。
。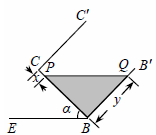
當液面恰好到達容器口沿,即點Q與點B′重合時,如圖,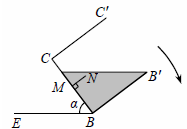
由BB′=4,且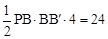 ,得PB=3,
,得PB=3,
∴由tan∠PB′B= ,得∠PB′B=37°。∴α=∠B′PB=53°。
,得∠PB′B=37°。∴α=∠B′PB=53°。
此時37°≤α≤53°。
延伸:當α=60°時,如圖所示,設FN∥EB,GB′∥EB,過點G作GH⊥BB′于點H。 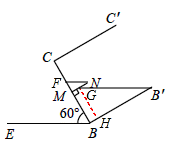
在Rt△B′GH中,GH=MB=2,∠GB′B=30°,
∴HB′=2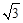 。
。
∴MG=BH=4-2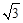 <MN。
<MN。
此時容器內液體形成兩層液面,液體的形狀分別是以Rt△NFM和直角梯形MBB′G為底面的直棱柱。
∵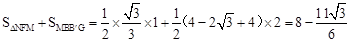 ,
,
∴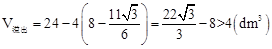 。
。
∴溢出液體可以達到4dm3


 奪冠金卷全能練考系列答案
奪冠金卷全能練考系列答案科目:初中數學 來源: 題型:
| 3 |
| 4 |
| 3 |
| 4 |


查看答案和解析>>
科目:初中數學 來源:2013年初中畢業升學考試(河北卷)數學(解析版) 題型:解答題
一透明的敞口正方體容器ABCD -A′B′C′D′ 裝有一些液體,棱AB始終在水平桌面上,容器底部的傾斜角為α (∠CBE = α,如圖1所示).
探究 如圖1,液面剛好過棱CD,并與棱BB′ 交于點Q,此時液體的形狀為直三棱柱,其三視圖及尺寸如
圖2所示.解決問題:
(1)CQ與BE的位置關系是 ,BQ的長是 dm;
(2)求液體的體積;(參考算法:直棱柱體積V液 = 底面積SBCQ×高AB)
(3)求α的度數.(注:sin49°=cos41°= ,tan37°=
,tan37°= )
)

拓展 在圖1的基礎上,以棱AB為軸將容器向左或向右旋轉,但不能使液體溢出,圖3或圖4是其正面示意圖.若液面與棱C′C或CB交于點P,設PC = x,BQ = y.分別就圖3和圖4求y與x的函數關系式,并寫出相應的α的范圍.

延伸 在圖4的基礎上,于容器底部正中間位置,嵌入一平行于側面的長方形隔板(厚度忽略不計),得到圖5,隔板高NM =" 1" dm,BM = CM,NM⊥BC.繼續向右緩慢旋轉,當α = 60°時,通過計算,判斷溢出容器的液體能否達到4 dm3.

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 ,tan37°=
,tan37°= )
)

查看答案和解析>>
科目:初中數學 來源:2013年河北省中考數學試卷(解析版) 題型:解答題
 ,tan37°=
,tan37°= )
)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com