
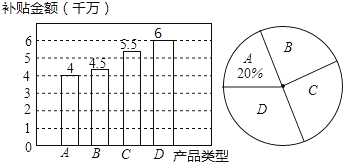
【題目】近幾年來,國家對購買新能源汽車實行補助政策,2016年某省對新能源汽車中的“插電式混合動力汽車”實行每輛3萬元的補助,小劉對該省2016年“純電動乘用車”和“插電式混合動力車”的銷售計劃進行了研究,繪制出如圖所示的兩幅不完整的統計圖.
(1)補全條形統計圖;
(2)求出“D”所在扇形的圓心角的度數;
(3)為進一步落實該政策,該省計劃再補助4.5千萬元用于推廣上述兩大類產品,請你預測,該省16年計劃大約共銷售“插電式混合動力汽車”多少輛?
注:R為純電動續航行駛里程,圖中A表示“純電動乘用車”(100km≤R<150km),B表示“純電動乘用車”(150km≤R<250km),C表示“純電動乘用車”(R≥250km),D為“插電式混合動力汽車”.
【答案】
(1)
解:補貼總金額為:4÷20%=20(千萬元),
則D類產品補貼金額為:20﹣4﹣4.5﹣5.5=6(千萬元),補全條形圖如圖:
(2)
解:360°× ![]() =108°,
=108°,
答:“D”所在扇形的圓心角的度數為108°
(3)
解:根據題意,16年補貼D類“插電式混合動力汽車”金額為:6+4.5× ![]() =7.35(千萬元),
=7.35(千萬元),
∴7350÷3=2450(輛),
答:預測該省16年計劃大約共銷售“插電式混合動力汽車”2450輛
【解析】(1)首先由A的數目和其所占的百分比可求出總數,進而可求出D的數目,問題得解;
(2)由D的數目先求出它所占的百分比,再用百分比乘以360°,即可解答;
(3)計算出補貼D類產品的總金額,再除以每輛車的補助可得車的數量.本題考查的是條形統計圖和扇形統計圖的綜合運用,讀懂統計圖,從不同的統計圖中得到必要的信息是解決問題的關鍵.條形統計圖能清楚地表示出每個項目的數據;扇形統計圖直接反映部分占總體的百分比大小.
【考點精析】解答此題的關鍵在于理解扇形統計圖的相關知識,掌握能清楚地表示出各部分在總體中所占的百分比.但是不能清楚地表示出每個項目的具體數目以及事物的變化情況,以及對條形統計圖的理解,了解能清楚地表示出每個項目的具體數目,但是不能清楚地表示出各個部分在總體中所占的百分比以及事物的變化情況.


科目:初中數學 來源: 題型:
【題目】八年級(1)班有48名學生,春游前,班長把全班學生對春游地點的意向繪制成了扇形統計圖,其中“想去動物園的學生數”的扇形圓心角為60°,則下列說法正確的是( )
A. 想去動物園的學生占全班學生的60% B. 想去動物園的學生有12人
C. 想去動物園的學生肯定最多 D. 想去動物園的學生占全班學生的![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有一內部裝有水的直圓柱形水桶,桶高20公分;另有一直圓柱形的實心鐵柱,柱高30公分,直立放置于水桶底面上,水桶內的水面高度為12公分,且水桶與鐵柱的底面半徑比為2:1.今小賢將鐵柱移至水桶外部,過程中水桶內的水量未改變,若不計水桶厚度,則水桶內的水面高度變為多少公分?( )
A.4.5
B.6
C.8
D.9
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD是一張邊長為12公分的皮革.皮雕師傅想在此皮革兩相鄰的角落分別切下△PDQ與△PCR后得到一個五邊形PQABR,其中PD=2DQ,PC=RC,且P、Q、
R三點分別在CD、AD、BC上,如圖所示.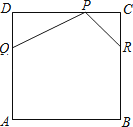
(1)當皮雕師傅切下△PDQ時,若DQ長度為x公分,請你以x表示此時△PDQ的面積.
(2)承(1),當x的值為多少時,五邊形PQABR的面積最大?請完整說明你的理由并求出答案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰直角△ABC中,∠ACB=90°,CO⊥AB于點O,點D、E分別在邊AC、BC上,且AD=CE,連結DE交CO于點P,給出以下結論:
①△DOE是等腰直角三角形;②∠CDE=∠COE;③若AC=1,則四邊形CEOD的面積為 ![]() ;④AD2+BE2﹣2OP2=2DPPE,其中所有正確結論的序號是
;④AD2+BE2﹣2OP2=2DPPE,其中所有正確結論的序號是
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,已知數軸上兩點A,B對應的數分別是﹣1,3,點P為數軸上的一動點,其對應的數為x

(1)A、B兩點的距離AB= ;
(2)在數軸上是否存在點P,使PA+PB=6?若存在,請求出x的值;若不存在,請說明理由.
(3)如圖2,若點P以每秒1個單位的速度從點O出發向右運動,同時點A以每秒5個單位的速度向左運動,點B以每秒20個單位的速度向右運動,在運動的過程中,M、N分別是AP、OB的中點,問:![]() 的值是否發生變化?請說明理由.
的值是否發生變化?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知點A、C在雙曲線![]() 上,點 B、D在雙曲線
上,點 B、D在雙曲線![]() 上,AD// BC//y 軸.
上,AD// BC//y 軸.
(I)當m=6,n=-3,AD=3 時,求此時點 A 的坐標;
(II)若點A、C關于原點O對稱,試判斷四邊形 ABCD的形狀,并說明理由;
(III)若AD=3,BC=4,梯形ABCD的面積為![]() ,求mn 的最小值.
,求mn 的最小值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,池塘邊有一塊長為18m,寬為10m的長方形土地,現在將其 余三面留出寬都是xm的小路,中間余下的長方形部分做菜地,用整式表示:
(1)菜地的長a= m,寬b= m;
(2)菜地面積S= m2;
(3)當x=0.5m時,菜地面積是多少?

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com