解:(1)相等;
證明如下:∵∠BAC=90°,AB=AC,
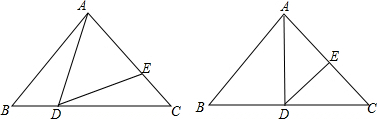
∴∠B=∠C=45°.如圖1,
∵∠1+∠B+∠ADB=180°,
∴∠1+∠ADB=180°-∠B=135°.
又∵∠2+∠ADE+∠ADB=180°,
∴∠2+∠ADB=180°-∠ADE
=180°-45°=135°,
即∠1+∠ADB=∠2+∠ADB,
∴∠1=∠2.

(2)由(1)知∠1=∠2,又∵∠B=∠C=45°,
∴△DCE∽△ABD.
若BD=x,則CD=BC-BD=2

-x,
由△DCE∽△ABD得

,即

,
CE=

(2

-x)x,
=-

x
2+

x,
y=AE=AC-CE=2-(-

x
2+

x)
∴y=

x
2-

x+2,
其中0<x<2

.
(3)解:∵點D不能與B點重合,∴AD=AE不能成立
(或:∵∠ADE=45°,若AD=AE,
則∠AED=ADE=45°,從而∠DAE=90°,
即B與D重合,這與已知條件矛盾).
①當AE、DE為腰,即AE=DE時(如圖2),
∠EAD=∠EDA=45°,此時,AD平分∠BAC,
∴D為BC邊的中點(“三線合一”性質),
且E也為AC邊的中點,∴AE=1;
②當AD、DE為腰,即AD=DE時(如圖3),
由(1)△ABD∽△DCE知,此時AD與DE為對應邊,
∴△ABD≌△DCE,DC=AB=2,
BD=BC-CD=2

-2,AE=AC-EC
=2-BD=2-(2

-2)=4-2

;
綜上所述,當△ADE是等腰三角形時,
AE的長為1或4-2

;
(4)不存在.
原因如下:∵△DCE∽△ABD,若△DCE的面積是△ABD面積的2倍,則
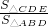
=2,
從而
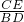
=

,CE=

BD,-

x
2+

x=

x,
解得x=0,即BD=0,就是說D點與B點重合,
這與已知條件矛盾,
∴不存在x,使△DCE的面積是△ABD面積的2倍.
分析:(1)由AB=AC易知△ABC是等腰直角三角形,即∠B=∠C=45°,已知∠ADE=45°,由三角形內角和定理以及平角的定義可得∠BAD、∠CDE都等于180°-45°-∠ADB,由此可證得兩角相等.
(2)由(1)的等角,聯立∠B=∠C=45°,可證得△DCE∽△ABD,根據相似三角形所得比例線段,即可表示出CE的長,進而由AE=AC-CE求得y、x的函數關系式.
(3)由于D與B、C不重合,顯然∠ADE=∠AED=45°不符合題意,即AD≠AE,所以此題分兩種情況討論:
①AD=DE,此時(2)的相似三角形全等,由此可求得CD、BD的長,進而可得CE、AE的值;
②AE=DE,此時∠DAE=45°,即AD平分∠BAC,由于△BAC是等腰直角三角形,根據等腰三角形三線合一的性質可知AD垂直平分BC,同理可證得DE垂直平分AC,即AE為AC長的一半,由此得解.
(4)若△DCE的面積是△ABD面積的2倍,根據相似三角形的面積比等于相似比的平方可知:CE=

BD,然后表示出AE的長,代入(2)的函數關系式中,即可求得x的值,若x=0,則說明D、B重合,顯然不存在符合條件的x,若x的值符合(2)的自變量取值范圍,那么x的值即為所求.
點評:此題主要考查了等腰直角三角形的性質以及相似三角形的判定和性質,同時還涉及到分類討論的數學思想,難度較大.

 E=45°,DE交AC于點E.
E=45°,DE交AC于點E.
 -x,
-x, ,即
,即 ,
, (2
(2 -x)x,
-x)x, x2+
x2+ x,
x, x2+
x2+ x)
x) x2-
x2- x+2,
x+2, .
. -2,AE=AC-EC
-2,AE=AC-EC -2)=4-2
-2)=4-2 ;
; ;
;
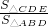 =2,
=2,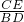 =
= ,CE=
,CE= BD,-
BD,- x2+
x2+ x=
x= x,
x, BD,然后表示出AE的長,代入(2)的函數關系式中,即可求得x的值,若x=0,則說明D、B重合,顯然不存在符合條件的x,若x的值符合(2)的自變量取值范圍,那么x的值即為所求.
BD,然后表示出AE的長,代入(2)的函數關系式中,即可求得x的值,若x=0,則說明D、B重合,顯然不存在符合條件的x,若x的值符合(2)的自變量取值范圍,那么x的值即為所求.


 如圖,Rt△ABC中,∠ACB=90°,tanB=
如圖,Rt△ABC中,∠ACB=90°,tanB= 如圖,Rt△ABC中,∠C=90°,△ABC的內切圓⊙0與BC、CA、AB分別切于點D、E、F.
如圖,Rt△ABC中,∠C=90°,△ABC的內切圓⊙0與BC、CA、AB分別切于點D、E、F.