
【題目】【新知理解】
如圖①,若點![]() 、
、![]() 在直線l同側,在直線l上找一點
在直線l同側,在直線l上找一點![]() ,使
,使![]() 的值最小.
的值最小.
作法:作點![]() 關于直線l的對稱點
關于直線l的對稱點![]() ,連接
,連接![]() 交直線l于點
交直線l于點![]() ,則點
,則點![]() 即為所求.
即為所求.
【解決問題】
如圖②,![]() 是邊長為6cm的等邊三角形
是邊長為6cm的等邊三角形![]() 的中線,點
的中線,點![]() 、
、![]() 分別在
分別在![]() 、
、![]() 上,則
上,則![]() 的最小值為 cm;
的最小值為 cm;
【拓展研究】
如圖③,在四邊形![]() 的對角線
的對角線![]() 上找一點
上找一點![]() ,使
,使![]() .(保留作圖痕跡,并對作圖方法進行說明)
.(保留作圖痕跡,并對作圖方法進行說明)

【答案】(1)![]() ;(2)作圖見解析.
;(2)作圖見解析.
【解析】試題分析:(1)作點E關于AD的對稱點F,連接PF,則PE=PF,根據兩點之間線段最短以及垂線段最短,得出當CF⊥AB時,PC+PE=PC+PF=CF(最短),最后根據勾股定理,求得CF的長即可得出PC+PE的最小值;
(2)根據軸對稱的性質進行作圖.
方法1:作B關于AC的對稱點E,連接DE并延長,交AC于P,連接BP,則∠APB=∠APD.
方法2:作點D關于AC的對稱點D',連接D'B并延長與AC的交于點P,連接DP,則∠APB=∠APD.
試題解析:(1)【解決問題】
如圖②,作點E關于AD的對稱點F,連接PF,則PE=PF,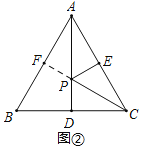
當點F,P,C在一條直線上時,PC+PE=PC+PF=CF(最短),
當CF⊥AB時,CF最短,此時BF=![]() AB=3(cm),
AB=3(cm),
∴Rt△BCF中,CF=![]() (cm),
(cm),
∴PC+PE的最小值為3![]() cm;
cm;
(2)【拓展研究】
方法1:如圖③,作B關于AC的對稱點E,連接DE并延長,交AC于P,點P即為所求,連接BP,則∠APB=∠APD.
方法2:如圖④,作點D關于AC的對稱點D',連接D'B并延長與AC的交于點P,點P即為所求,連接DP,則∠APB=∠APD.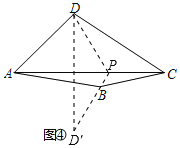


科目:初中數學 來源: 題型:
【題目】如圖,在平面直接坐標系中,有若干個橫坐標分別為整數的點,其順序按圖中(1,0)→(2,0)→(2,1)→(1,1)→(1,2)→(2,2)…根據這個規律,則第2016個點的橫坐標為( )

A. 44 B. 45 C. 46 D. 47
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數y=kx+b 的圖象與反比例函數y=![]() 的圖交象于A、B兩點,且點A的橫坐標和點B的縱坐標都是-2 , 求:
的圖交象于A、B兩點,且點A的橫坐標和點B的縱坐標都是-2 , 求:
(1)一次函數的解析式;
(2)△AOB的面積
查看答案和解析>>
科目:初中數學 來源: 題型:
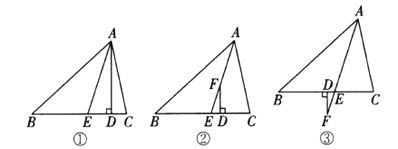
【題目】在![]() 中,
中,![]() .如圖①,
.如圖①,![]() 于點
于點![]() ,
,![]() 平分
平分![]() ,則易知
,則易知![]() .
.
(1)如圖②,![]() 平分
平分![]() ,
, ![]() 為
為![]() 上的一點,且
上的一點,且![]() 于點
于點![]() ,這時
,這時![]() 與
與![]() 、
、![]() 有何數量關系?請說明理由;
有何數量關系?請說明理由;
(2)如圖③,![]() 平分
平分![]() ,
,![]() 為
為![]() 延長線上的一點,
延長線上的一點,![]() 于點
于點![]() ,請你寫出這時
,請你寫出這時![]() 與
與![]() 、
、![]() 之間的數量關系(只寫結論,不必說明理由).
之間的數量關系(只寫結論,不必說明理由).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數學實驗課上,李靜同學剪了兩張直角三角形紙片,進行如下的操作:
操作一:如圖1,將Rt△ABC紙片沿某條直線折疊,使斜邊兩個端點A與B重合,折痕為DE.
(1)如果AC=5cm,BC=7cm,可得△ACD的周長為 ;
(2)如果∠CAD:∠BAD=1:2,可得∠B的度數為 ;
操作二:如圖2,李靜拿出另一張Rt△ABC紙片,將直角邊AC沿直線CD折疊,使點A與點E重合,若AB=10cm,BC=8cm,請求出BE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了鍛煉學生身體素質,訓練定向越野技能,某校在一公園內舉行定向越野挑戰賽.路線圖如圖![]() 所示,點
所示,點![]() 為矩形
為矩形![]() 邊
邊![]() 的中點,在矩形
的中點,在矩形![]() 的四個頂點處都有定位儀,可監測運動員的越野進程,其中一位運動員
的四個頂點處都有定位儀,可監測運動員的越野進程,其中一位運動員![]() 從點
從點![]() 出發,沿著
出發,沿著![]() 的路線勻速行進,到達點
的路線勻速行進,到達點![]() .設運動員
.設運動員![]() 的運動時間為
的運動時間為![]() ,到監測點的距離為
,到監測點的距離為![]() .現有
.現有![]() 與
與![]() 的函數關系的圖象大致如圖
的函數關系的圖象大致如圖![]() 所示,則這一信息的來源是( ).
所示,則這一信息的來源是( ).


A. 監測點![]() B. 監測點
B. 監測點![]() C. 監測點
C. 監測點![]() D. 監測點
D. 監測點![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
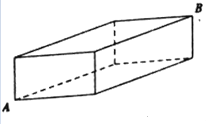
【題目】如圖,長方體的長、寬、高分別為6cm,4cm,2cm,現有一只螞蟻點A出發,沿長方體表面達到B處,則所走的最短路徑是 __________ cm。
查看答案和解析>>
科目:初中數學 來源: 題型:
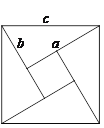
【題目】如圖①,美麗的弦圖,蘊含著四個全等的直角三角形.
(1)弦圖中包含了一大,一小兩個正方形,已知每個直角三角形較長的直角邊為![]() ,較短的直角邊為
,較短的直角邊為![]() ,斜邊長為
,斜邊長為![]() ,試利用圖①驗證勾股定理;
,試利用圖①驗證勾股定理;
(2)如圖②,將這四個全等的直角三角形緊密地拼接,形成飛鏢狀,已知外圍輪廓(實線)的周長為![]() ,
, ![]() ,求該飛鏢狀圖案的面積;
,求該飛鏢狀圖案的面積;
(3)如圖③,將八個全等的直角三角形緊密地拼接,記圖中正方形![]() ,正方形
,正方形![]() ,正方形
,正方形![]() 的面積分別為
的面積分別為![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,則
,則![]() =________.
=________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com