
【題目】某學校以隨機抽樣的方式開展了中學生喜歡數學的程度的問卷調查,調查的結果分為A(不喜歡)、B(一般)、C(比較喜歡)、D(非常喜歡)四個等級,圖1、圖2是根據采集的數據繪制的兩幅不完整的統計圖.
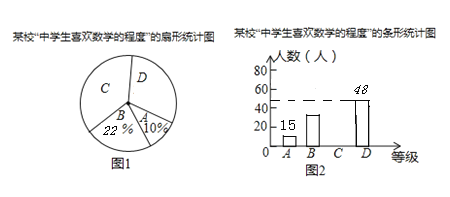
(1)本次抽樣調查的樣本容量是;
(2)請直接在圖2中補全C對應的條形統計圖;
(3)若該校有學生1000人,請根據調查結果,估計“比較喜歡”的學生人數為多少人.
 開心試卷期末沖刺100分系列答案
開心試卷期末沖刺100分系列答案 雙基同步導航訓練系列答案
雙基同步導航訓練系列答案 黃岡小狀元同步計算天天練系列答案
黃岡小狀元同步計算天天練系列答案科目:初中數學 來源: 題型:
【題目】下面是小明主設計的“作一個含30°角的直角三角形”的尺規作圖過程.
已知:直線l.
![]()
求作:△ABC,使得∠ACB=90°,∠ABC=30°.
作法:如圖,
![]()
①在直線l上任取兩點O,A;
②以點O為圓心,OA長為半徑畫弧,交直線l于點B;
③以點A為圓心,AO長為半徑畫弧,交![]() 于點C;
于點C;
④連接AC,BC.
所以△ABC就是所求作的三角形.
根據小明設計的尺規作圖過程:
(1)使用直尺和圓規,補全圖形;(保留作圖痕跡)
(2)完成下面的證明.
證明:在⊙O中,AB為直徑,
∴∠ACB=90°(① ),(填推理的依據)
連接OC
∵OA=OC=AC,
∴∠CAB=60°,
∴∠ABC=30°(② ),(填推理的依據)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一名大學畢業生利用“互聯網+”自主創業,銷售一種產品,這種產品的成本價為80元/件,經市場調查發現,該產品的日銷售量![]() (單位:件)與銷售單價
(單位:件)與銷售單價![]() (單位:元/件)之間滿足一次函數關系,如圖所示.
(單位:元/件)之間滿足一次函數關系,如圖所示.
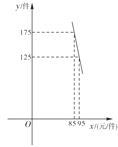
(1)求![]() 與
與![]() 之間的函數解析式,并寫出自變量
之間的函數解析式,并寫出自變量![]() 的取值范圍;
的取值范圍;
(2)求每天的銷售利潤![]() (單位:元)與銷售單價
(單位:元)與銷售單價![]() 之間的函數關系式,并求出每件銷售單價為多少元時,每天的銷售利潤最大?最大利潤是多少?
之間的函數關系式,并求出每件銷售單價為多少元時,每天的銷售利潤最大?最大利潤是多少?
(3)這名大學生計劃開展科技創新,以降低該產品的成本,預計在今后的銷售中,日銷售量與銷售單價仍存在(1)中的關系.若想實現銷售單價為90元時,日銷售利潤不低于3750元的銷售目標,該產品的成本單價應不超過多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知反比例函數 y=![]() 的圖像經過點A(-1,a),過點A作AB⊥x軸,垂足為點B,△AOB的面積為
的圖像經過點A(-1,a),過點A作AB⊥x軸,垂足為點B,△AOB的面積為![]() .
.
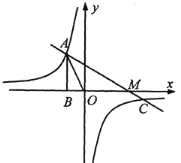
(1)求a、k的值;
(2)若一次函數y=mx+n圖像經過點A和反比例函數圖像上另一點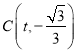 ,且與x軸交于M點,求AM的值:
,且與x軸交于M點,求AM的值:
(3)在(2)的條件下,如果以線段AM為一邊作等邊△AMN,頂點N在一次數函數y=bx上,則b= ______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】《九章算術》是中國傳統數學最重要的著作,奠定了中國傳統數學的基本框架.它的代數成就主要包括開方術、正負術和方程術.其中,方程術是《九章算術》最高的數學成就.《九章算術》中記載:“今有甲乙二人持錢不知其數.甲得乙半而錢五十,乙得甲太半而錢亦五十.問甲、乙持錢各幾何?”
譯文:“假設有甲乙二人,不知其錢包里有多少錢.若乙把自己一半的錢給甲,則甲的錢數為50;而甲把自己![]() 的錢給乙,則乙的錢數也能為50.問甲、乙各有多少錢?”
的錢給乙,則乙的錢數也能為50.問甲、乙各有多少錢?”
設甲持錢為x,乙持錢為y,可列方程組為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列結論:①abc>0;②2a+b=0;③若m為任意實數,則a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,則x1+x2=2.其中,正確結論的個數為( )
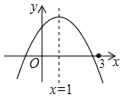
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某文具店銷售甲、乙兩種圓規,當銷售5只甲種、1只乙種圓規,可獲利潤25元,銷售6只甲種、3只乙種圓規,可獲利潤39元.
(1)問該文具店銷售甲、乙兩種圓規,每只的利潤分別是多少元?
(2)在(1)中,文具店共銷售甲、乙兩種圓規50只,其中甲種圓規為a只,求文具店所獲得利潤P與a的函數關系式,并求當a≥30時P的最大值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com