
【題目】如圖,CA⊥AB,垂足為 A,AB=24,AC=12,射線 BM⊥AB,垂足為 B, 一動點 E 從 A點出發以 3 厘米/秒沿射線 AN 運動,點 D 為射線 BM 上一動點, 隨著 E 點運動而運動,且始終保持 ED=CB,當點 E 經過______秒時,△DEB 與△BCA 全等.

科目:初中數學 來源: 題型:
【題目】如圖1,二次函數y= ![]() x2+bx+c與一次函數y=
x2+bx+c與一次函數y= ![]() x﹣3的圖象都經過x軸上點A(4,0)和y軸上點B(0,﹣3),過動點M(m,0)(0<m<4)作x軸的垂線交直線AB于點C,交拋物線于點P.
x﹣3的圖象都經過x軸上點A(4,0)和y軸上點B(0,﹣3),過動點M(m,0)(0<m<4)作x軸的垂線交直線AB于點C,交拋物線于點P.
(1)求b,c的值;
(2)點M在運動的過程中,能否使△PBC為直角三角形?如果能,求出點P的坐標;如果不能,請說明理由;
(3)如圖2,過點P作PD⊥AB于點,設△PCD的面積為S1 , △ACM的面積為2 , 若 ![]() =
= ![]() ,
,
①求m的值;
②如圖3,將線段OM繞點O順時針旋轉得到OM′,旋轉角為α(0°<α<90°),連接M'A、M'B,求M'A+ ![]() M'B的最小值.
M'B的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數學課上,老師提出如下問題:已知:線段a,b(如圖1).
求作:等腰△ABC,使AB=AC,BC=a,BC邊上的高為b.
小姍的作法如下:如圖2,
(i)作線段BC=a;
(ii)作線段BC的垂直平分線MN交線段BC于點D;
(iii)在MN上截取線段DA=b,連接AB,AC.所以,△ABC就是所求作的等腰三角形.
老師說:“小姍的作法正確”.
請回答:得到△ABC是等腰三角形的依據是: .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,∠ABC=90°,DE⊥AC于點E,且AE=CE,DE=5,EB=12. 
(1)求AD的長;
(2)若∠CAB=30°,求四邊形ABCD的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC 中,BO 平分∠ABC,CO 平分∠ACB,MN 經過點 O,與 AB、AC 相交于點 M、N,且 MN∥BC,那么下列說法中:①∠MOB=∠MBO②△AMN 的周長等于 AB+AC;③∠A=2∠BOC﹣180°;④連接 AO,則![]() :
:![]() :
:![]() =AB:AC:BC;正確的有( )
=AB:AC:BC;正確的有( )
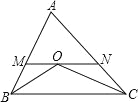
A. ①②④ B. ①②③ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E 是 BC 的中點,DE 平分∠ADC.
(1)如圖 1,若∠B=∠C=90°,求證:AE 平分∠DAB;
(2)如圖 2,若 DE⊥AE,求證:AD=AB+CD.
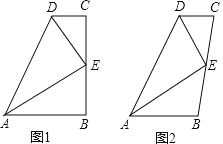
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們用![]() 表示不大于
表示不大于![]() 的最大整數,例如:
的最大整數,例如:![]() ,
,![]() ,
,![]() ;用
;用![]() 表示大于
表示大于![]() 的最小整數,例如:
的最小整數,例如:![]() ,
,![]() ,
,![]() .解決下列問題:
.解決下列問題:
(1)![]() = ,,
= ,,![]() = ;
= ;
(2)若![]() =2,則
=2,則![]() 的取值范圍是 ;若
的取值范圍是 ;若![]() =-1,則
=-1,則![]() 的取值范圍是 ;
的取值范圍是 ;
(3)已知![]() ,
,![]() 滿足方程組
滿足方程組![]() ,求
,求![]() ,
,![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程或方程組解應用題: 在某場CBA比賽中,某位運動員的技術統計如表所示:
技術 | 上場時間(分鐘) | 出手投籃(次) | 投中 | 罰球得分(分) | 籃板 | 助攻(次) | 個人總得分(分) |
數據 | 38 | 27 | 11 | 6 | 3 | 4 | 33 |
注:(i)表中出手投籃次數和投中次數均不包括罰球;
(ii)總得分=兩分球得分+三分球得分+罰球得分.
根據以上信息,求本場比賽中該運動員投中兩分球和三分球各幾個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在學習貫徹十九大精神“我學習,我踐行”的活動中,計劃組織全校1300名師生到林業部門規劃的林區植樹,經研究,決定租用當地出租車公司提供的![]() 兩種型號的客車共50輛作為交通工具,下表是租車公司提供給學校有關兩種型號客車的載客量與租車信息:
兩種型號的客車共50輛作為交通工具,下表是租車公司提供給學校有關兩種型號客車的載客量與租車信息:
型號 | 載客量 | 租金單價 |
| 30人/輛 | 300元/輛 |
| 20人/輛 | 240元/輛 |
注:載客量指的是每輛車客車最多可載該校師生的人數
(1)設租用![]() 型號客車
型號客車![]() 輛,租車總費用
輛,租車總費用![]() 元,求
元,求![]() 與
與![]() 的函數解析式,并直接寫出
的函數解析式,并直接寫出![]() 的取值范圍;
的取值范圍;
(2)若要使租車總費用不超過13980元,一共有幾種租車方案?哪種租車方案最省錢?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com