
【題目】數學課上,老師給出了如下問題:如圖,∠AOB=80°,OC平分∠AOB,若∠BOD=20°.
(1)請你補全圖形,并求∠COD的度數;
(2)若∠BOD=![]() 其他條件不變,請直接寫出∠COD的度數.
其他條件不變,請直接寫出∠COD的度數.

【答案】(1)60°或20°;(2)40°+β或|40°-β|.
【解析】
(1)分兩種情況討論:①當OD在OB的下方時,由OC為角平分線求出∠BOC度數,根據∠BOC+∠BOD即可求出∠COD的度數;②當OD在OB的上方時,由OC為角平分線求出∠BOC度數,根據∠BOC﹣∠BOD即可求出∠COD的度數.
(2)根據(1),類似的分兩種情況討論即可.
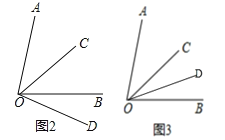
(1)分兩種情況討論:①當OD在OB的下方時,如圖2.
∵OC平分∠AOB,∠AOB=80°,∴∠BOC![]() ∠AOB=40°.
∠AOB=40°.
∵∠BOD=20°,∴∠COD=∠BOC+∠BOD=40°+20°=60°.
②當OD在OB的上方時,如圖3.
∵OC平分∠AOB,∠AOB=80°,∴∠BOC![]() ∠AOB=40°.
∠AOB=40°.
∵∠BOD=20°,∴∠COD=∠BOC﹣∠BOD=40°﹣20°=20°.
綜上所述:∠COD的度數為60°或20°.
(2)根據(1)可得:∠COD的度數為40°+β或|40°-β|.


 應用題天天練四川大學出版社系列答案
應用題天天練四川大學出版社系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c的圖象如圖,其對稱軸為直線x=1,給出下列結論: ①b2﹣4ac>0;②2a+b=0;③abc>0;④3a+c>0,
則正確的結論個數為( )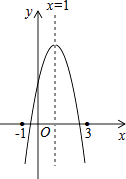
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某城鎮中學學做家務的時間,一綜合實踐活動小組對該班50名學生進行了調查,根據調查所得的數據制成如下圖的頻數分布直方圖.
(1)補全該圖,并寫出相應的頻數;
(2)求第1組的頻率;
(3)求該班學生每周做家務時間的平均數;
(4)你的做家務時間在哪一組內?請用一句話談談你的感受.
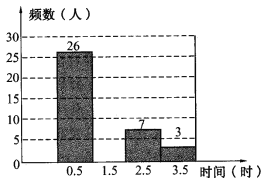
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在“3·15”消費者權益日的活動中,對甲、乙兩家商場售后服務的滿意度進行了抽查.如圖反映了被抽查用戶對兩家商場售后服務的滿意程度(以下稱:用戶滿意度),分為很不滿意、不滿意、較滿意、很滿意四個等級,并依次記為1分、2分、3分、4分.
(1)分別求出甲、乙兩商場的用戶滿意度分數的平均值(計算結果精確到0.01).
(2)請你根據所學的統計知識,判斷哪家商場的用戶滿意度較高,并簡要說明理由.
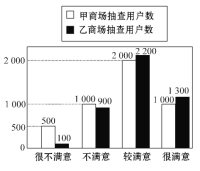
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系中,O為坐標原點,拋物線y=a(x﹣h)2﹣4(a>0)與x軸分別交于原點O、A兩點,點A在x軸的正半軸上,頂點為D,直線y= ![]() x交拋物線于B點,過B作BE∥x軸交拋物線另一點E,交對稱軸于F.
x交拋物線于B點,過B作BE∥x軸交拋物線另一點E,交對稱軸于F.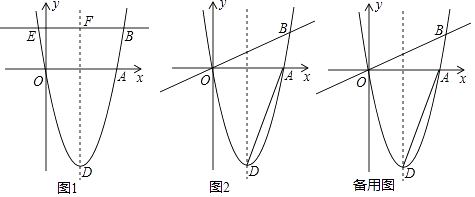
(1)當DF=4a時,求BE的長.
(2)如圖2,連AD,連接AD繞點A旋轉交直線OB于點G,點D的對應點為G,當OG=2時,求a的值;
(3)在(2)的條件下,當0<a<1時,以OB為直徑作圓交x軸下方拋物線于點P,求點P坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖a、圖b是兩張形狀、大小完全相同的方格紙,方格紙中每個小正方形的邊長均為1,點A、B在小正方形的頂點上.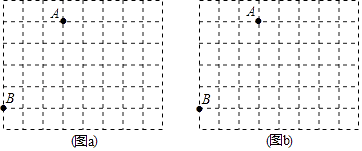
(1)在圖a中畫出△ABC(點C在小正方形的頂點上),使△ABC是等腰三角形且△ABC為鈍角三角形;
(2)在圖b中畫出△ABD(點D在小正方形的頂點上),使△ABD是等腰三角形,且tan∠ABD=1.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD是平行四邊形,下列說法不正確的是( )
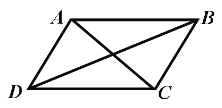
A. 當AC=BD時,四邊形ABCD是矩形
B. 當AB=BC時,四邊形ABCD是菱形
C. 當AC⊥BD時,四邊形ABCD是菱形
D. 當∠DAB=90°時,四邊形ABCD是正方形
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com