
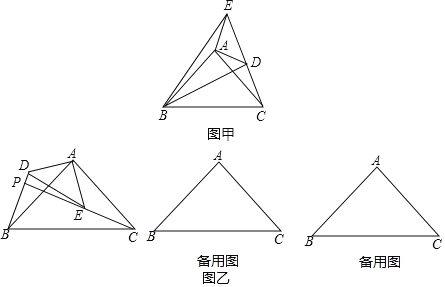
【題目】如圖乙,△ABC 和△ADE 是有公共頂點的等腰直角三角形,∠BAC=∠DAE=90°,點P為射線 BD,CE的交點.
(1)如圖甲,將△ADE 繞點A 旋轉,當 C、D、E 在同一條直線上時,連接BD、BE,則下列給出的四個結論中,其中正確的是哪幾個.(回答直接寫序號)
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2)
(2)若 AB=4,AD=2,把△ADE 繞點 A 旋轉,
①當∠CAE=90°時,求 PB 的長;
②直接寫出旋轉過程中線段 PB 長的最大值.
【答案】(1)①②③;(2)①PB=![]() 或
或![]() ,②PB長的最小值是
,②PB長的最小值是![]() -2,最大值是
-2,最大值是![]() +2.
+2.
【解析】
(1)①由條件證明△ABD≌△ACE,就可以得到結論②由△ABD≌△ACE就可以得出∠ABD=∠ACE,就可以得出∠BDC=90°,進而得出結論;③由條件知∠ABC=∠ABD+∠DBC=45°,由∠ABD=∠ACE就可以得出結論;④△BDE為直角三角形就可以得出BE2=BD2+DE2,由△DAE和△BAC是等腰直角三角形就有DE2=2AD2,BC2=2AB2,就有BC2=BD2+CD2≠BD2就可以得出結論;
(2)①分兩種情形a、如圖乙-1中,當點E在AB上時,BE=AB-AE=2.由△PEB∽△AEC,得![]() =
=![]() ,由此即可解決問題.b、如圖乙-2中,當點E在BA延長線上時,BE=6.解法類似;
,由此即可解決問題.b、如圖乙-2中,當點E在BA延長線上時,BE=6.解法類似;
②如圖乙-3中,以A為圓心AD為半徑畫圓,當CE在⊙A上方與⊙A相切時,PB的值最大.分別求出PB即可.
(1)①②③;
(2)①解:a、如圖2中,當點E在AB上時,BE=AB-AE=2.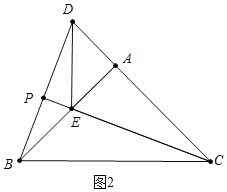
∵∠EAC=90°,
∴CE=![]() ,
,
同(1)可證△ADB≌△AEC.
∴∠DBA=∠ECA.
∵∠PEB=∠AEC,
∴△PEB∽△AEC.
∴![]() ,
,
∴![]() ,
,
∴PB=![]()
b、如圖3中,當點E在BA延長線上時,BE=6.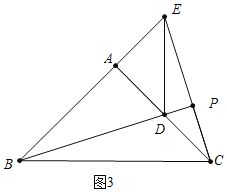
∵∠EAC=90°,
∴CE=![]() ,
,
同(1)可證△ADB≌△AEC.
∴∠DBA=∠ECA.
∵∠BEP=∠CEA,
∴△PEB∽△AEC,
∴![]() ,
,
∴![]() ,
,
∴PB=![]() ,
,
綜上,PB=![]() 或
或![]() .
.
②解:a、如圖4中,以A為圓心AD為半徑畫圓,當CE在⊙A下方與⊙A相切時,PB的值最小.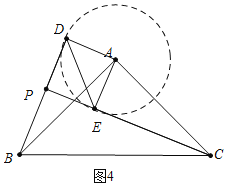
理由:此時∠BCE最小,因此PB最小,(△PBC是直角三角形,斜邊BC為定值,∠BCE最小,因此PB最小)
∵AE⊥EC,
∴EC=![]() ,
,
由(1)可知,△ABD≌△ACE,
∴∠ADB=∠AEC=90°,BD=CE=2![]() ,
,
∴∠ADP=∠DAE=∠AEP=90°,
∴四邊形AEPD是矩形,
∴PD=AE=2,
∴PB=BD-PD=2![]() -2.
-2.
b、如圖5中,以A為圓心AD為半徑畫圓,當CE在⊙A上方與⊙A相切時,PB的值最大.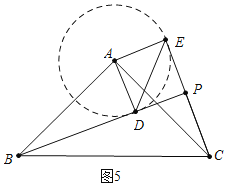
理由:此時∠BCE最大,因此PB最大,(△PBC是直角三角形,斜邊BC為定值,∠BCE最大,因此PB最大)
∵AE⊥EC,
∴EC=![]() ,
,
由(1)可知,△ABD≌△ACE,
∴∠ADB=∠AEC=90°,BD=CE=![]() ,
,
∴∠ADP=∠DAE=∠AEP=90°,
∴四邊形AEPD是矩形,
∴PD=AE=2,
∴PB=BD+PD=![]() +2.
+2.
綜上所述,PB長的最小值是![]() -2,最大值是
-2,最大值是![]() +2.
+2.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,并且關于x的一元二次方程ax2+bx+c﹣m=0有兩個不相等的實數根,下列結論:
①b2﹣4ac<0;②abc>0;③a﹣b+c<0;④m>﹣2,
其中,正確的個數有( )
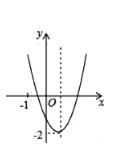
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】 今年清明節前后某茶葉銷售商在青山茶廠先后購進兩批茶葉.第一批茶葉進貨用了5.4萬元,進貨單價為a元/千克.購回后該銷售商將茶葉分類包裝出售,把其中300千克精裝品以進貨單件的兩倍出售;余下的簡裝品以150元/千克的價格出售,全部賣出.第二批進貨用了5萬元,這一次的進貨單價每千克比第一批少了20元.購回分類包裝后精裝品占總質量的一半,以200元/千克的單價出售;余下的簡裝品在這批進貨單價的基礎上每千克加價40元后全部賣出.若其它成本不計,第二批茶葉獲得的毛利潤是3.5萬元.
(1)用含a的代數式表示第一批茶葉的毛利潤;
(2)求第一批茶葉中精裝品每千克售價.(總售價-總進價=毛利潤)
查看答案和解析>>
科目:初中數學 來源: 題型:
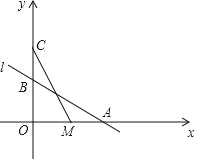
【題目】如圖,直線l:y=﹣![]() x+2與x軸,y軸分別交于點A,B,在y軸上有一點C(0,4),動點M從點A出發以毎秒1個単位長度的速度沿x軸向左運動,設運動的時間為t秒.
x+2與x軸,y軸分別交于點A,B,在y軸上有一點C(0,4),動點M從點A出發以毎秒1個単位長度的速度沿x軸向左運動,設運動的時間為t秒.
(1)求點A的坐標;
(2)請從A,B兩題中任選一題作答.
A.求△COM的面積S與時間t之間的函數表達式;
B.當△ABM為等腰三角形時,求t的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了解某校九年級學生的理化實驗操作情況,隨機抽查了40名同學實驗操作的得分.根據獲取的樣本數據,制作了如下的條形統計圖和扇形統計圖.請根據相關信息,解答下列問題:
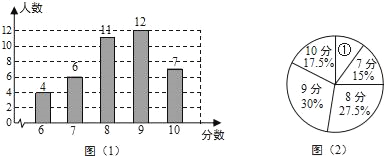
(Ⅰ)扇形 ①的圓心角的大小是 ;
(Ⅱ)求這40個樣本數據的平均數、眾數、中位數;
(Ⅲ)若該校九年級共有320名學生,估計該校理化實驗操作得滿分(10分)有多少人.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知O為坐標原點,拋物線y1=ax2+bx+c(a≠0)與x軸相交于點A(x1,0),B(x2,0),與y軸交于點C,且O,C兩點間的距離為3,x1x2<0,|x1|+|x2|=4,點A,C在直線y2=﹣3x+t上.
(1)當y1隨著x的增大而增大時,求自變量x的取值范圍;
(2)將拋物線y1向左平移n(n>0)個單位,記平移后y隨著x的增大而增大的部分為P,直線y2向下平移n個單位,當平移后的直線與P有公共點時,求2n2﹣5n的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為宣傳節約用水,小強隨機調查了某小區部分家庭3月份的用水情況,并將收集的數據整理成如下統計圖.
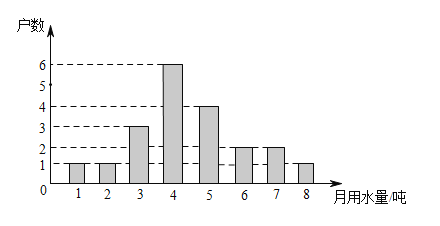
(1)小明一共調查了多少戶家庭?
(2)求所調查家庭3月份用水量的眾數、中位數和平均數;
(3)若該小區有800戶居民,請你估計這個小區3月份的總用水量是多少噸?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 在平面直角坐標系中的位置如圖所示,且三個頂點都在正方形網格的格點上.
在平面直角坐標系中的位置如圖所示,且三個頂點都在正方形網格的格點上.
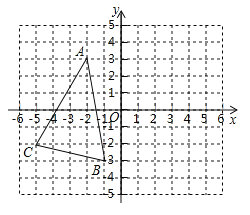
(1)把![]() 沿
沿![]() 軸翻折得到
軸翻折得到![]() ,畫出
,畫出![]() ,并寫出點
,并寫出點![]() 的坐標_____;
的坐標_____;
(2)若點![]() 在
在![]() 內部,當
內部,當![]() 沿
沿![]() 軸翻折后,點
軸翻折后,點![]() 對應點
對應點![]() 的坐標是_____;
的坐標是_____;
(3)求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學開展“八榮八恥”演講比賽活動,九(1)、九(2)班根據初賽成績各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績(滿分為100分)如下圖所示.

(1)根據下圖,分別求出兩班復賽的平均成績和方差;
(2)根據(1)的計算結果,分析哪個班級的復賽成績較好?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com