
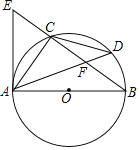
【題目】如圖,⊙O是Rt△ABC的外接圓,∠ACB=90°,點D是![]() 上的一點,且
上的一點,且![]() ,連接AD交BC于點F,過點A作⊙O的切線AE交BC的延長線于點E.
,連接AD交BC于點F,過點A作⊙O的切線AE交BC的延長線于點E.
(1)求證:CF=CE;
(2)若AD=8,AC=5,求⊙O的半徑.
【答案】(1)見解析;(2)![]()
【解析】
(1)根據切線的性質和圓周角定理得到∠CAE=∠B,∠DAC=∠B,即可得到∠CAE=∠CAF,然后通過證得△CAE≌△CAF即可證得結論;
(2)連接OC,則根據垂徑定理得到OC⊥AD,AH=DH,根據勾股定理求得CH=3,設⊙O的半徑為r,在Rt△AOH中,OA2=AH2+OH2,得到r2=42+(r﹣3)2,解得即可.
(1)證明:∵∠ACB=90°,
∴AB是⊙O的直徑,AC⊥EF,
∵AE是⊙O的切線,
∴∠CAE=∠B,
∵![]() ,
,
∴∠DAC=∠B,
∴∠CAE=∠CAF,
在△CAE和△CAF中
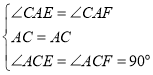
∴△CAE≌△CAF(SAS),
∴CF=CE;
(2)解:連接OC,交AD于H,
∵![]() ,
,
∴OC⊥AD,AH=DH,
∵AD=8,AC=5,
∴AH=4,
在Rt△ACH中,CH=![]() =3,
=3,
設⊙O的半徑為r,
∴OH=r﹣3,
在Rt△AOH中,OA2=AH2+OH2,
∴r2=42+(r﹣3)2,
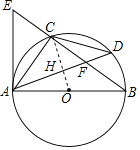
解得r=![]()


 口算心算速算應用題系列答案
口算心算速算應用題系列答案 同步拓展閱讀系列答案
同步拓展閱讀系列答案科目:初中數學 來源: 題型:
【題目】學校準備開辦“書畫、器樂、戲曲、棋類”四個興趣班.為了解學生對興趣班的選擇情況,隨機抽取部分學生調查.每人單選一項,結果如下(尚未完善).
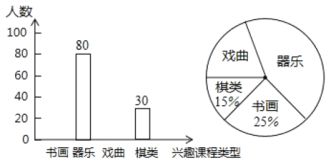
![]() 求本次調查的學生人數和扇形圖中“器樂”對應圓心角的大小.
求本次調查的學生人數和扇形圖中“器樂”對應圓心角的大小.
![]() 若全校共有
若全校共有![]() 名學生,請估計選擇“戲曲”的人數.
名學生,請估計選擇“戲曲”的人數.
![]() 學校將從四個興趣班中任選取兩個參加全區青少年才藝展示活動,求恰好抽到“器樂”和“戲曲”的概率.
學校將從四個興趣班中任選取兩個參加全區青少年才藝展示活動,求恰好抽到“器樂”和“戲曲”的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
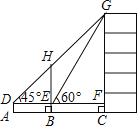
【題目】如圖,某數學興趣小組利用一棵古樹BH測量教學樓CG的高,先在A處用高1.5米的測角儀測得古樹頂端H的仰角∠HDE為45°,此時教學樓頂端G恰好在視線DH上,再向前走7米到達B處,又測得教學樓頂端G的仰角∠GEF為60°,點A、B、C三點在同一水平線上.計算教學樓CG的高.(結果精確到0.1,參考數據:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標中,拋物線y=ax2+bx+c過點A(﹣1,0),B(3,0),C(0,3),點P是直線BC上方拋物線上的一動點,PE∥y軸,交直線BC于點E連接AP,交直線BC于點 D.
(1)求拋物線的函數表達式;
(2)當AD=2PD時,求點P的坐標;
(3)求線段PE的最大值;
(4)當線段PE最大時,若點F在直線BC上且∠EFP=2∠ACO,直接寫出點F的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
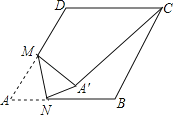
【題目】如圖,在邊長為2的菱形ABCD中,∠A=60°,M是AD邊的中點,N是AB邊上的一動點,將△AMN沿MN所在直線翻折得到△A′MN,連接A′C,則A′C長度的最小值是_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
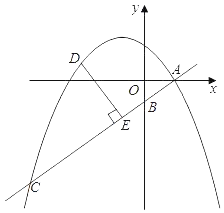
【題目】如圖,在平面直角坐標系中,直線y=kx﹣![]() 與拋物線y=ax2+bx+
與拋物線y=ax2+bx+![]() 交于點A、C,與y軸交于點B,點A的坐標為(2,0),點C的橫坐標為﹣8.
交于點A、C,與y軸交于點B,點A的坐標為(2,0),點C的橫坐標為﹣8.
(1)請直接寫出直線和拋物線的解析式;
(2)點D是直線AB上方的拋物線上一動點(不與點A、C重合),作DE⊥AC于點E.設點D的橫坐標為m.求DE的長關于m的函數解析式,并寫出DE長的最大值;
(3)平移△AOB,使平移后的三角形的三個頂點中有兩個在拋物線上,請直接寫出平移后的點A對應點A′的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
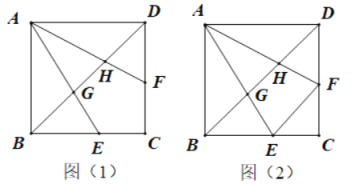
【題目】如圖(1),已知正方形ABCD中,點E、F分別在邊BC、CD上,BE=DF,AE、AF分別交BD于點G、H.
(1)求證:BG=DH;
(2)連接FE,如圖(2),當EF=BG時.
①求證:ADAH=AFDF;
②直接寫出![]() 的比值.
的比值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形ABCD,點M是邊BA延長線上的動點(不與點A重合),且AM<AB,△CBE由△DAM平移得到.若過點E作EH⊥AC,H為垂足,則有以下結論:①點M位置變化,使得∠DHC=60°時,2BE=DM;②無論點M運動到何處,都有DM=![]() HM;③無論點M運動到何處,∠CHM一定大于135°.其中正確結論的序號為_____.
HM;③無論點M運動到何處,∠CHM一定大于135°.其中正確結論的序號為_____.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com