
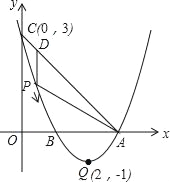
【題目】如圖,已知拋物線y=ax2+bx+c(a≠0)的頂點坐標為Q(2,﹣1),且與y軸交于點C(0,3),與x軸交于A,B兩點(點A在點B的右側),點P是該拋物線上的一動點,從點C沿拋物線向點A運動(點P與A不重合),過點P作PD∥y軸,交AC于點D.
(1)求該拋物線的函數關系式;
(2)當△ADP是直角三角形時,求點P的坐標;
(3)在題(2)的結論下,若點E在x軸上,點F在拋物線上,問是否存在以A、P、E、F為頂點的平行四邊形?若存在,求點F的坐標;若不存在,請說明理由.
【答案】(1) y=x2﹣4x+3;(2) P1(1,0),P2(2,﹣1);(3) F1(2﹣![]() ,1),F2(2+
,1),F2(2+![]() ,1).
,1).
【解析】試題分析:(1)已知了拋物線的頂點坐標,可將拋物線的解析式設為頂點式,然后將函數圖象經過的C點坐標代入上式中,即可求出拋物線的解析式;
(2)由于PD∥y軸,所以∠ADP≠90°,若△ADP是直角三角形,可考慮兩種情況:
①以點P為直角頂點,此時AP⊥DP,此時P點位于x軸上(即與B點重合),由此可求出P點的坐標;
②以點A為直角頂點,易知OA=OC,則∠OAC=45°,所以OA平分∠CAP,那么此時D、P關于x軸對稱,可求出直線AC的解析式,然后設D、P的橫坐標,根據拋物線和直線AC的解析式表示出D、P的縱坐標,由于兩點關于x軸對稱,則縱坐標互為相反數,可據此求出P點的坐標;
(3)很顯然當P、B重合時,不能構成以A、P、E、F為頂點的四邊形,因為點P、F都在拋物線上,且點P為拋物線的頂點,所以PF與x軸不平行,所以只有(2)②的一種情況符合題意,由②知此時P、Q重合;假設存在符合條件的平行四邊形,那么根據平行四邊形的性質知:P、F的縱坐標互為相反數,可據此求出F點的縱坐標,代入拋物線的解析式中即可求出F點的坐標.
試題解析:(1)∵拋物線的頂點為Q(2,﹣1),
∴設拋物線的解析式為y=a(x﹣2)2﹣1,
將C(0,3)代入上式,得:
3=a(0﹣2)2﹣1,a=1;
∴y=(x﹣2)2﹣1,即y=x2﹣4x+3;
(2)分兩種情況:
①當點P1為直角頂點時,點P1與點B重合;
令y=0,得x2﹣4x+3=0,解得x1=1,x2=3;
∵點A在點B的右邊,
∴B(1,0),A(3,0);
∴P1(1,0);
②當點A為△AP2D2的直角頂點時;
∵OA=OC,∠AOC=90°,
∴∠OAD2=45°;
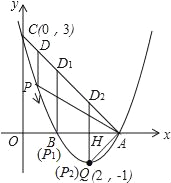
當∠D2AP2=90°時,∠OAP2=45°,
∴AO平分∠D2AP2;
又∵P2D2∥y軸,
∴P2D2⊥AO,
∴P2、D2關于x軸對稱;
設直線AC的函數關系式為y=kx+b(k≠0).
將A(3,0),C(0,3)代入上式得:
![]() ,
,
解得![]() ;
;
∴y=﹣x+3;
設D2(x,﹣x+3),P2(x,x2﹣4x+3),
則有:(﹣x+3)+(x2﹣4x+3)=0,
即x2﹣5x+6=0;
解得x1=2,x2=3(舍去);
∴當x=2時,y=x2﹣4x+3=22﹣4×2+3=﹣1;
∴P2的坐標為P2(2,﹣1)(即為拋物線頂點).
∴P點坐標為P1(1,0),P2(2,﹣1);
(3)由(2)知,當P點的坐標為P1(1,0)時,不能構成平行四邊形;
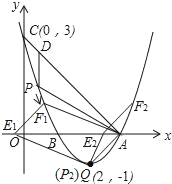
當點P的坐標為P2(2,﹣1)(即頂點Q)時,
平移直線AP交x軸于點E,交拋物線于F;
∵P(2,﹣1),
∴可設F(x,1);
∴x2﹣4x+3=1,
解得x1=2﹣![]() ,x2=2+
,x2=2+![]() ;
;
∴符合條件的F點有兩個,
即F1(2﹣![]() ,1),F2(2+
,1),F2(2+![]() ,1).
,1).


 新課標階梯閱讀訓練系列答案
新課標階梯閱讀訓練系列答案 口算心算速算應用題系列答案
口算心算速算應用題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,等腰直角三角形OA1A2的直角邊OA1在y軸的正半軸上,且OA1=A1A2=1,以OA2為直角邊作第二個等腰直角三角形OA2A3,以OA3為直角邊作第三個等腰直角三角形OA3A4,…,依此規律,得到等腰直角三角形OA2017A2018,則點A2017的坐標為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
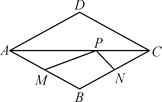
【題目】點P是菱形ABCD的對角線AC上的一個動點,已知AB=1,∠ADC=120°, 點M,N分別是AB,BC邊上的中點,則△MPN的周長最小值是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某年5月,我國南方某省A、B兩市遭受嚴重洪澇災害,1.5萬人被迫轉移,鄰近縣市C、D獲知A、B兩市分別急需救災物資200噸和300噸的消息后,決定調運物資支援災區.已知C市有救災物資240噸,D市有救災物資260噸,現將這些救災物資全部調往A、B兩市.已知從C市運往A、B兩市的費用分別為每噸20元和25元,從D市運往往A、B兩市的費用分別為每噸15元和30元,設從C市運往B市的救災物資為x噸.
(1)請填寫下表;
A | B | 合計(噸) | |
C |
| x | 240 |
D |
|
| 260 |
總計(噸) | 200 | 300 | 500 |
(2)設C、D兩市的總運費為W元,求W與x之間的函數關系式,并寫出自變量x的取值范圍;
(3)經過搶修,從C市到B市的路況得到了改善,縮短了運輸時間,運費每噸減少n元(N>0),其余路線運費不變,若C、D兩市的總運費的最小值不小于10080元,求n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某國際化學校實行小班制教學,七年級四個班共有學生(6m-3n)人,一班有學生m人,二班人數比一班人數的兩倍少n人,三班人數比二班人數的一半多12人.
(1)求三班的學生人數(用含m.n的式子表示);
(2)求四班的學生人數;(用含m.n的式子表示);
(3)若四個班共有學生120人,求二班比三班多的學生人數?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,甲和乙同時從學校放學,兩人以各自送度勻速步行回家,甲的家在學校的正西方向,乙的家在學校的正東方向,乙家離學校的距離比甲家離學校的距離遠3900米,甲準備一回家就開始做什業,打開書包時發現錯拿了乙的練習冊.于是立即步去追乙,終于在途中追上了乙并交還了練習冊,然后再以先前的速度步行回家,(甲在家中耽擱和交還作業的時間忽略不計)結果甲比乙晚回到家中,如圖是兩人之間的距離y米與他們從學校出發的時間x分鐘的函數關系圖,則甲的家和乙的家相距_____米.

查看答案和解析>>
科目:初中數學 來源: 題型:
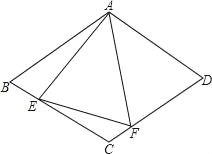
【題目】如圖,在菱形ABCD中,AB=4,∠BAD=120°,△AEF為正三角形,E、F在菱形的邊BC,CD上.
(1)證明:BE=CF.
(2)當點E,F分別在邊BC,CD上移動時(△AEF保持為正三角形),請探究四邊形AECF的面積是否發生變化?若不變,求出這個定值;如果變化,求出其最大值.
(3)在(2)的情況下,請探究△CEF的面積是否發生變化?若不變,求出這個定值;如果變化,求出其最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖直線y=2x+m與y=![]() (n≠0)交于A,B兩點,且點A的坐標為(1,4).
(n≠0)交于A,B兩點,且點A的坐標為(1,4).
(1)求此直線和雙曲線的表達式;
(2)過x軸上一點M作平行于y軸的直線1,分別與直線y=2x+m和雙曲線y=![]() (n≠0)交于點P,Q,如果PQ=2QM,求點M的坐標.
(n≠0)交于點P,Q,如果PQ=2QM,求點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系xOy中,已知點A(0,3)、點B(3,0),一次函數y=2x的圖象與直線AB交于點M.
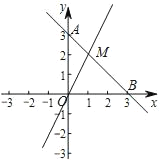
(1)求直線AB的函數解析式及M點的坐標;
(2)若點N是x軸上一點,且△MNB的面積為6,求點N的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com