
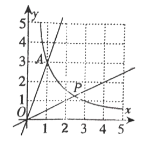
【題目】如圖,反比例函數![]() 的圖象過格點(網格線的交點)
的圖象過格點(網格線的交點)![]() .
.
(1)求反比例函數的解析式;
(2)若點![]() 是該雙曲線第一象限上的一點,且
是該雙曲線第一象限上的一點,且![]() ,
,
填空:①直線![]() 的解析式為_______;②點
的解析式為_______;②點![]() 的坐標為______.
的坐標為______.
【答案】(1)![]() ;(2)①
;(2)①![]() ,②
,②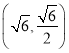
【解析】
(1)把格點A(1,3)代入解析式即可得到答案.(2)①過O作OA的垂線構造出兩組全等三角形,得到B(3,-1)及AC=BC,求出點C的橫坐標為3,用AC=BC建立方程求解即可得出結論; ②聯立直線OP和雙曲線解析式,解得即可得出結論.
解:(1)![]() 反比例函數
反比例函數![]() 的圖象過格點
的圖象過格點![]() ,
,![]() ,
,
![]() 反比例函數的解析式為
反比例函數的解析式為![]() ;
;
(2)①如圖,過點O作OA的垂線OE,取![]() 軸上點(3,0), 記D,則D(3,0),過A作
軸上點(3,0), 記D,則D(3,0),過A作![]() 軸與
軸與![]() ,而
,而![]() ,
,![]() ,
,
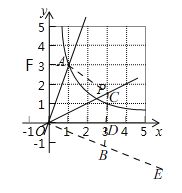
![]() 過點D作BD⊥
過點D作BD⊥![]() 軸,交OE于B,OP于C,
軸,交OE于B,OP于C,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ≌
≌![]() ,
,![]() ,
,![]()
![]() ,
,
![]() ,
, ![]()
∴![]() ≌
≌![]() , ∴
, ∴![]() ,
,
設![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴ ![]() , ∴
, ∴![]() ,
,
∴![]() , 設直線OP的解析式為
, 設直線OP的解析式為![]() ,
,
∴![]() , ∴
, ∴![]() ,
,
∴直線OP的解析式為![]() ,
,
故答案為:![]() ;
;
②由①知,直線OP的解析式為![]() ,
,
由(1)知,反比例函數解析式為![]() ,
,
所以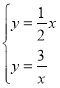 , 解得:
, 解得: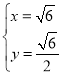 或
或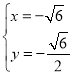
(由于點P在第一象限內,所以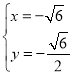 ,舍去),
,舍去),
∴![]() ,
,
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,直線AB、CD相交于點O,∠AOC=30°,半徑為2cm的P的圓心在射線OA上,且與點O的距離為6cm,如果P以1cm/s的速度沿直線AB由A向B的方向移動,那么P與直線CD相切時☉P運動的時間是( )
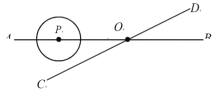
A.3秒或10秒B.3秒或8秒C.2秒或8秒D.2秒或10秒
查看答案和解析>>
科目:初中數學 來源: 題型:
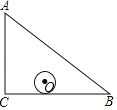
【題目】如圖,在△ABC中,AC:BC:AB=3:4:5,⊙O沿著△ABC的內部邊緣滾動一圈,若⊙O的半徑為1,且圓心O運動的路徑長為18,則△ABC的周長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
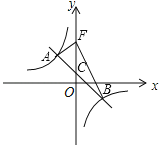
【題目】在平面直角坐標系中,一次函數y=﹣x+b的圖象與反比例函數y=![]() (k≠0)的圖象交于A、B點,與y軸交于點C,其中點A的半標為(﹣2,3)
(k≠0)的圖象交于A、B點,與y軸交于點C,其中點A的半標為(﹣2,3)
(1)求一次函數和反比例函數的解析式;
(2)如圖,若將點C沿y軸向上平移4個單位長度至點F,連接AF、BF,求△ABF的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
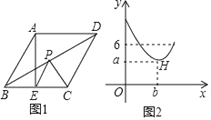
【題目】如圖1,在菱形ABCD中,∠A=120°,點E是BC邊的中點,點P是對角線BD上一動點,設PD的長度為x,PE與PC的長度和為y,圖2是y關于x的函數圖象,其中H是圖象上的最低點,則a+b的值為( )
A.7![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,等邊△ABC中D點為AB邊上一動點,E為直線AC上一點,將△ADE沿著DE折疊,點A落在直線BC上,對應點為F,若AB=4,BF:FC=1:3,則線段AE的長度為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是二次函數y=ax2+bx+c(a,b,c是常數,a≠0)圖象的一部分,與x軸的交點A在點(2,0)和(3,0)之間,對稱軸是x=1.對于下列說法:①ab<0;②2a+b=0;③3a+c>0;④a+b≥m(am+b)(m為實數);⑤當﹣1<x<3時,y>0,其中正確的是( )

A. ①②④ B. ①②⑤ C. ②③④ D. ③④⑤
查看答案和解析>>
科目:初中數學 來源: 題型:
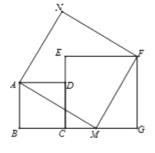
【題目】勾股定理歷史悠久,三國時期的趙爽證明了勾股定理,后人借助“趙爽弦圖”,用三個正方形證明勾股定理,如圖所示,B,C,M,G在同一條直線上,四邊形ABCD,四邊形CEFG,四邊形AMFN都為正方形,若五邊形ABGFN的面積為34,CM=2,則△ABM的面積為( )
A.10B.![]() C.5D.4
C.5D.4
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com