
【題目】已知∠AOB=120°,OC、OD過點O的射線,射線OM、ON分別平分∠AOC和∠DOB.
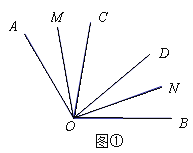
(1)如圖①,若OC、OD是∠AOB 的三等分線,求∠MON的度數;
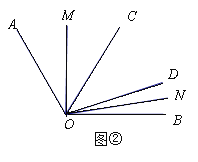
(2)如圖②,若∠COD=50°,∠AOC≠∠DOB,則∠MON= °;
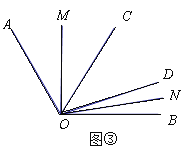
(3)如圖③,在∠AOB內,若∠COD=α(0°<α<60°),則∠MON= °.
【答案】(1)∠MON =80°;(2)85°;(3)![]()
【解析】試題分析:(1)根據角平分線的定義得到∠AOC=∠COD=∠DOB=![]() ×120°=40°,∠MOC=∠AOC=20°,∠DON=∠DOB=20°,則∠MON=20°+40°+20°=80°;
×120°=40°,∠MOC=∠AOC=20°,∠DON=∠DOB=20°,則∠MON=20°+40°+20°=80°;
(2)根據角平分線的定義得到∠MOC=![]() ∠AOC,∠DON=
∠AOC,∠DON=![]() ∠DOB,而∠AOC+∠DOB=120°-50°=70°,則∠MOC+∠DON=35°,所以∠MON=50°+35°=85°;
∠DOB,而∠AOC+∠DOB=120°-50°=70°,則∠MOC+∠DON=35°,所以∠MON=50°+35°=85°;
(3)與(2)一樣得到∠AOC+∠DOB=120°-α,∠MOC+∠DON=60°-![]() α,則∠MON=60°-
α,則∠MON=60°-![]() α+α=60°+
α+α=60°+![]() α.
α.
試題解析:(1)∵OC,OD是∠AOB的三等分線,
∴∠AOC=∠COD=∠DOB=![]() ∠AOB=
∠AOB=![]() ×120°=40°,
×120°=40°,
∵OM平分∠AOC,ON平分∠DOB,
∴∠MOC=![]() ∠AOC=20°, ∠DON=
∠AOC=20°, ∠DON=![]() ∠DOB=20° ,
∠DOB=20° ,
∴∠MON=∠MOC+∠COD+∠DON=80°;
(2)∵射線OM、ON分別平分∠ACO和∠DOB,
∴∠MOC=![]() ∠AOC,∠DON=
∠AOC,∠DON=![]() ∠DOB,
∠DOB,
∴∠MOC+∠DON=![]() (∠AOC+∠DOB),
(∠AOC+∠DOB),
∵∠AOB=120°,∠COD=50°,
∴∠AOC+∠DOB=120°-50°=70°,
∴∠MOC+∠DON=35°,
∴∠MON=50°+35°=85°,
故答案為:85;
(3)∵射線OM、ON分別平分∠AOC和∠DOB,
∴∠MOC=![]() ∠AOC,∠DON=
∠AOC,∠DON=![]() ∠DOB,
∠DOB,
∴∠MOC+∠DON=![]() (∠AOC+∠DOB),
(∠AOC+∠DOB),
∵∠AOB=120°,∠COD=α,
∴∠AOC+∠DOB=120°-α,
∴∠MOC+∠DON=60°-![]() α,
α,
∴∠MON=60°-![]() α+α=60°+
α+α=60°+![]() α=
α=![]() ,
,
故答案為: ![]() .
.


科目:初中數學 來源: 題型:
【題目】陳老師和學生做一個猜數游戲,他讓學生按照如下步驟進行計算:
①任想一個兩位數a,把a乘以2,再加上9,把所得的和再乘以2;
②把a乘以2,再加上30,把所得的和除以2;
③把①所得的結果減去②所得的結果,這個差即為最后的結果.
陳老師說:只要你告訴我最后的結果,我就能猜出你最初想的兩位數a.
學生周曉曉計算的結果是96,陳老師立即猜出周曉曉最初想的兩位數是31.
請完成
(1)由①可列代數式 ,由②可列代數式 ,由③可知最后結果為 ;(用含a的式子表示)
(2)學生小明計算的結果是120,你能猜出他最初想的兩位數是多少嗎?
(3)請用自己的語言解釋陳老師猜數的方法.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:點A,B,C在同一條直線上,點M、N分別是AB、AC的中點,如果AB=10cm,AC=8cm,那么線段MN的長度為( )
A. 6cm B. 9cm C. 3cm或6cm D. 1cm或9cm
查看答案和解析>>
科目:初中數學 來源: 題型:
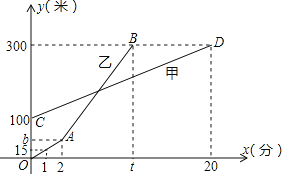
【題目】甲、乙兩人相約周末登花果山,甲、乙兩人距地面的高度y(米)與登山時間x(分)之間的函數圖象如圖所示,根據圖象所提供的信息解答下列問題:
(1)甲登山上升的速度是每分鐘 米,乙在A地時距地面的高度b為 米.
(2)若乙提速后,乙的登山上升速度是甲登山上升速度的3倍,請求出乙登山全程中,距地面的高度y(米)與登山時間x(分)之間的函數關系式.
(3)登山多長時間時,甲、乙兩人距地面的高度差為50米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在解決數學問題的過程中,我們常用到 “分類討論”的數學思想,下面是運用分類討論的數學思想解決問題的過程,請仔細閱讀,并解答問題.
【提出問題】三個有理數![]() 滿足
滿足![]() ,求
,求![]() 的值.
的值.
【解決問題】
解:由題意,得![]() 三個有理數都為正數或其中一個為正數,另兩個為負數.
三個有理數都為正數或其中一個為正數,另兩個為負數.
①![]() 都是正數,即
都是正數,即![]() 時,則
時,則![]() ;
;
②當![]() 中有一個為正數,另兩個為負數時,不妨設
中有一個為正數,另兩個為負數時,不妨設![]() ,則
,則![]() .
.
綜上所述, ![]() 值為3或-1.
值為3或-1.
【探究】請根據上面的解題思路解答下面的問題:
(1)三個有理數![]() 滿足
滿足![]() ,求
,求![]() 的值;
的值;
(2)若![]() 為三個不為0的有理數,且
為三個不為0的有理數,且![]() ,求
,求![]() 的值
的值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com