
【題目】歐幾里得在《幾何原本》中,記載了用圖解法解方程![]() 的方法,類似地可以用折紙的方法求方程
的方法,類似地可以用折紙的方法求方程![]() 的一個正根。下面是甲、乙兩位同學的做法:甲:如圖1,裁一張邊長為1的正方形的紙片
的一個正根。下面是甲、乙兩位同學的做法:甲:如圖1,裁一張邊長為1的正方形的紙片![]() ,先折出
,先折出![]() 的中點
的中點![]() ,再折出線段
,再折出線段![]() ,然后通過折疊使
,然后通過折疊使![]() 落在線段
落在線段![]() 上,折出點
上,折出點![]() 的新位置
的新位置![]() ,因而
,因而![]() ,類似地,在
,類似地,在![]() 上折出點
上折出點![]() 使
使![]() 。此時,
。此時,![]() 的長度可以用來表示方程
的長度可以用來表示方程![]() 的一個正根;乙:如圖2,裁一張邊長為1的正方形的紙片
的一個正根;乙:如圖2,裁一張邊長為1的正方形的紙片![]() ,先折出
,先折出![]() 的中點
的中點![]() ,再折出線段
,再折出線段![]() N,然后通過沿線段
N,然后通過沿線段![]() 折疊使
折疊使![]() 落在線段
落在線段![]() 上,折出點
上,折出點![]() 的新位置
的新位置![]() ,因而
,因而![]() 。此時,
。此時,![]() 的長度可以用來表示方程
的長度可以用來表示方程![]() 的一個正根;甲、乙兩人的做法和結果( )。
的一個正根;甲、乙兩人的做法和結果( )。

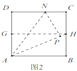
A.甲對,乙錯B.乙對,甲錯C.甲乙都對D.甲乙都錯
科目:初中數學 來源: 題型:
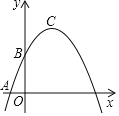
【題目】在平面直角坐標系xOy中(如圖).已知拋物線y=﹣![]() x2+bx+c經過點A(﹣1,0)和點B(0,
x2+bx+c經過點A(﹣1,0)和點B(0,![]() ),頂點為C,點D在其對稱軸上且位于點C下方,將線段DC繞點D按順時針方向旋轉90°,點C落在拋物線上的點P處.
),頂點為C,點D在其對稱軸上且位于點C下方,將線段DC繞點D按順時針方向旋轉90°,點C落在拋物線上的點P處.
(1)求這條拋物線的表達式;
(2)求線段CD的長;
(3)將拋物線平移,使其頂點C移到原點O的位置,這時點P落在點E的位置,如果點M在y軸上,且以O、D、E、M為頂點的四邊形面積為8,求點M的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
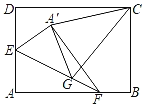
【題目】如圖,在矩形紙片ABCD中,AB=8,BC=6,點E是AD的中點,點F是AB上一動點.將△AEF沿直線EF折疊,點A落在點A'處.在EF上任取一點G,連接GC,GA',CA’,則△CGA'的周長的最小值為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
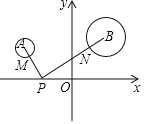
【題目】如圖,平面直角坐標系中,分別以點A (﹣2,3),B(3,4)為圓心,以1、2為半徑作⊙A、⊙B,M、N分別是⊙A、⊙B上的動點,P為x軸上的動點,則PM+PN的最小值等于( )
A.![]() B.
B.![]() +3C.
+3C.![]() ﹣3D.3
﹣3D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
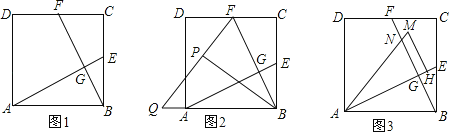
【題目】如圖1,在正方形ABCD中,E,F分別為BC,CD的中點,連接AE,BF,交點為G.若正方形的邊長為2.
(1)求證:AE⊥BF;
(2)將△BCF沿BF對折,得到△BPF(如圖2),延長FP交BA的延長線于點Q,求AQ的長;
(3)將△ABE繞點A逆時針方向旋轉,使邊AB正好落在AE上,得到△AHM(如圖3),若AM和BF相交于點N,求四邊形MNGH的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某風景區內的公路如圖1所示,景區內有免費的班車,從入口處出發,沿該公路開往草甸,途中停靠塔林(上下車時間忽略不計).第一班車上午8點發車,以后每隔10分鐘有一班車從入口處發車.小聰周末到該風景區游玩,上午7:40到達入口處,因還沒到班車發車時間,于是從景區入口處出發,沿該公路步行25分鐘后到達塔林.離入口處的路程![]() (米)與時間
(米)與時間![]() (分)的函數關系如圖2所示.
(分)的函數關系如圖2所示.
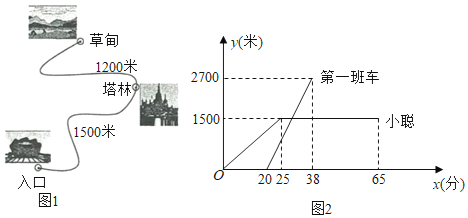
(1)求第一班車離入口處的路程![]() (米)與時間
(米)與時間![]() (分)的函數表達式.
(分)的函數表達式.
(2)求第一班車從人口處到達塔林所蓄的時間.
(3)小聰在塔林游玩40分鐘后,想坐班車到草甸,則小聘聰最早能夠坐上第幾班車?如果他坐這班車到草甸,比他在塔林游玩結束后立即步行到草甸提早了幾分鐘?(假設每一班車速度均相同,小聰步行速度不變)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為發展學生的核心素養,培養學生的綜合能力,某學校計劃開設四門選修課:樂器、舞蹈、繪畫、書法.學校采取隨機抽樣的方法進行問卷調查(每個被調查的學生必須選擇而且只能選擇其中一門).對調查結果進行整理,繪制成如下兩幅不完整的統計圖,請結合圖中所給信息解答下列問題:
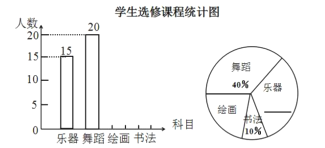
(1)補全條形統計圖,補全扇形統計圖中樂器所占的百分比;
(2)本次調查學生選修課程的“眾數”是__________;
(3)若該校有1200名學生,請估計選修繪畫的學生大約有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,在平面直角坐標系![]() 中,直線
中,直線![]() 分別交
分別交![]() 軸,
軸,![]() 軸于
軸于![]() ,
,![]() 兩點.點
兩點.點![]() 的坐標為
的坐標為![]() ,拋物線
,拋物線![]() 經過
經過![]() ,
,![]() 兩點.
兩點.
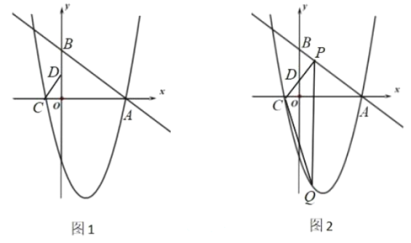
(1)求拋物線的表達式;
(2)如圖1,![]() 是線段
是線段![]() 上一點,連接
上一點,連接![]() ,若
,若![]() 的值最小,求
的值最小,求![]() 點坐標;
點坐標;
(3)如圖2,在(2)的前提下,直線![]() 與直線
與直線![]() 的交點為
的交點為![]() ,過
,過![]() 點作
點作![]() 軸的平行線交拋物線于點
軸的平行線交拋物線于點![]() ,若
,若![]() 是拋物線上一點,
是拋物線上一點,![]() 是
是![]() 軸上一點,是否存在以
軸上一點,是否存在以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點且
為頂點且![]() 為邊的平行四邊形,若存在,求出
為邊的平行四邊形,若存在,求出![]() 點坐標;若不存在,說明理由.
點坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com