
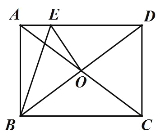
【題目】如圖,矩形 ABCD 的對角線 AC 與 BD 交于點 O,點 E 在 AD 上,且 DE=CD,連接 OE,BE, ABE ![]() ACB ,若 AE=2,則 OE 的長為___________.
ACB ,若 AE=2,則 OE 的長為___________.
【答案】![]()
【解析】
作∠ACB的平分線CG交BE于G,AC與BE交于點F,首先證明CB=CF,AF=AE=2,然后在Rt△ABC中利用勾股定理構建方程求出DE=CD=AB=6,BC=CF=AD=8,BD=AC=10,過點E作EH⊥BD于H,證明△EHD∽△BAD,利用相似三角形的性質求出EH和DH,進而可得OH,再利用勾股定理求OE即可.
解:作∠ACB的平分線CG交BE于G,AC與BE交于點F,
∵ABE=![]() ACB,GCB=
ACB,GCB=![]() ACB,
ACB,
∴ABE=GCB,
∵ABE+∠EBC=90°,
∴GCB+∠GBC=90°,
∴CG⊥BE,
∵CG平分∠ACB,
∴CB=CF,
∴∠FBC=∠BFC=∠AFE,
∵AD∥BC,
∴∠AEF=∠FBC,
∴∠AEF=∠AFE,
∴AF=AE=2,
設DE=CD=AB=x,則BC=CF=AD=x+2,AC=x+2+2=x+4,
在Rt△ABC中,AB2+BC2=AC2,即x2+(x+2)2=(x+4)2,
解得:x=6(負值已舍去),
∴DE=CD=AB=6,BC=CF=AD=8,BD=AC=10,
過點E作EH⊥BD于H,
∵∠EHD=∠BAD,∠EDH=∠BDA,
∴△EHD∽△BAD,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,![]() ,
,
∴OH=OD-DH=![]() BD-DH=
BD-DH=![]() ,
,
∴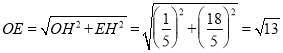 ,
,
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】觀察下列兩個等式:2﹣![]() =2×
=2×![]() +1,5﹣
+1,5﹣![]() =5×
=5×![]() +1,給出定義如下
+1,給出定義如下
我們稱使等式a﹣b=ab+1成立的一對有理數“a,b”為共生有理數對”,記為(a,b)
(1)通過計算判斷數對“﹣2,1”,“4,![]() ”是不是“共生有理數對”;
”是不是“共生有理數對”;
(2)若(6,a)是“共生有理數對”,求a的值;
(3)若(m,n)是“共生有理數對”,則“﹣n,﹣m” “共生有理數對”(填“是”或“不是”),并說明理由;
(4)若(m,n)是“共生有理數對”(其中n≠1),直接用含n的代數式表示m.
查看答案和解析>>
科目:初中數學 來源: 題型:
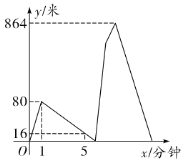
【題目】疫情之下,中華兒女共抗時艱.重慶和湖北同飲長江水,為更好地馳援武漢,打贏防疫攻堅戰,我市某公益組織收集社會捐獻物資.甲、乙兩人先后從![]() 地沿相同路線出發徒步前往
地沿相同路線出發徒步前往![]() 地進行物資捐獻,甲出發1分鐘后乙再出發,一段時間后乙追上甲,這時甲發現有東西落在
地進行物資捐獻,甲出發1分鐘后乙再出發,一段時間后乙追上甲,這時甲發現有東西落在![]() 地,于是原路原速返回
地,于是原路原速返回![]() 地去取(甲取東西的時間忽略不計),而乙繼續前行,甲乙兩人到達B地后原地幫忙.已知在整個過程中,甲乙均保持各自的速度勻速行走,甲、乙兩人相距的路程
地去取(甲取東西的時間忽略不計),而乙繼續前行,甲乙兩人到達B地后原地幫忙.已知在整個過程中,甲乙均保持各自的速度勻速行走,甲、乙兩人相距的路程![]() (米)與甲出發的時間
(米)與甲出發的時間![]() (分鐘)之間的函數關系如圖所示,則當乙到達
(分鐘)之間的函數關系如圖所示,則當乙到達![]() 地時,甲距
地時,甲距![]() 地的路程是_______米.
地的路程是_______米.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,將
,將![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 后得到
后得到![]() ,將線段
,將線段![]() 繞點
繞點![]() 逆時針旋轉
逆時針旋轉![]() 后得到線段
后得到線段![]() ,分別以
,分別以![]() 、
、![]() 為圓心,
為圓心,![]() 、
、![]() 長為半徑畫弧
長為半徑畫弧![]() 和弧
和弧![]() ,連接
,連接![]() ,則圖中陰影部分的面積是________.
,則圖中陰影部分的面積是________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:△ABC 內接于⊙O,過點 A 作⊙O 的切線交 CB 的延長線于點 P,且∠PAB=45°.
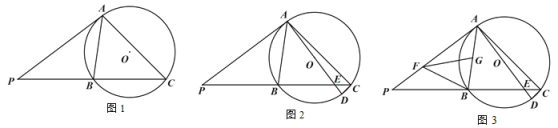
(1)如圖 1,求∠ACB 的度數;
(2)如圖 2,AD 是⊙O 的直徑,AD 交 BC 于點 E,連接 CD,求證:AC CD ![]() ;
;
(3)如圖 3 ,在(2)的條件下,當 BC 4![]() CD 時,點 F,G 分別在 AP,AB 上,連接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的長.
CD 時,點 F,G 分別在 AP,AB 上,連接 BF,FG,∠BFG=∠P,且 BF=FG,若 AE=15,求 FG 的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著科技的進步和網絡資源的豐富,在線學習已經成為更多人的自主學習選擇.某校計劃為學生提供以下四類在線學習方式:在線閱讀、在線聽課、在線答題和在線討論.為了解學生需求,該校隨機對本校部分學生進行了“你對哪類在線學習方式最感興趣”的調查,并根據調查結果繪制成如下兩幅不完整的統計圖.
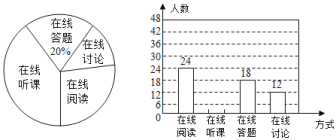
(1)求本次調查的學生總人數,并補全條形統計圖;
(2)求扇形統計圖中“在線討論”對應的扇形圓心角的度數;
(3)該校共有學生2100人,請你估計該校對在線閱讀最感興趣的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】每年4月23日是世界讀書日,某校為了解學生課外閱讀情況,隨機抽取![]() 名學生,對每人每周用于課外閱讀的平均時間(單位:
名學生,對每人每周用于課外閱讀的平均時間(單位:![]() )進行調查,過程如下:
)進行調查,過程如下:
收集數據:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
整理數據:
課外閱讀平均時間 |
|
|
|
|
等級 |
|
|
|
|
人數 |
|
|
|
|
分析數據:
平均數 | 中位數 | 眾數 |
|
|
|
請根據以上提供的信息,解答下列問題:
(1)填空:![]() ;
;![]() ;
;![]() ;
;![]() ;
;
(2)已知該校學生![]() 人,若每人每周用于課外閱讀的平均時間不少于
人,若每人每周用于課外閱讀的平均時間不少于![]() 為達標,請估計達標的學生數;
為達標,請估計達標的學生數;
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com