
【題目】如圖,拋物線y=-![]() +
+![]() +4的圖象與y軸交于點A,與x軸交于B、C兩點,其對稱軸與x軸交于點D,連接AC.
+4的圖象與y軸交于點A,與x軸交于B、C兩點,其對稱軸與x軸交于點D,連接AC.
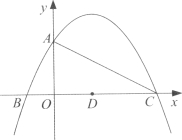
(1)點A的坐標為_______ ,點C的坐標為_______ ;
(2)線段AC上是否存在點E,使得△EDC為等腰三角形?若存在,求出所有符合條件的點E的坐標;若不存在,請說明理由;
(3)點P為x軸上方的拋物線上的一個動點,連接PA、PC,若所得△PAC的面積為S,則S取何值時,相應的點P有且只有2個?
【答案】(1)、A(0,4) C(8,0);(2)、![]() (0,4)、
(0,4)、![]() 、
、![]() (8-2
(8-2![]() ,
,![]() );(3)、S=16.
);(3)、S=16.
【解析】
試題分析:(1)、根據x=0和y=0分別求出點A和點C的坐標;(2)、首先求出點D的坐標,CD的長度和直線AC的解析式,然后分DE=DC,DE=EC和DC=EC三種情況分別求出點E的坐標;(3)、首先設出點P和點Q的坐標,然后列出面積的函數關系式,然后進行求解.
試題解析:(1)、A(0,4) C(8,0)
(2)、易得D(3,0),CD=5, 設直線AC對應的函數關系式為y=kx+b,則:![]()
解得: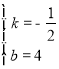 ; ∴y=-
; ∴y=-![]() x+4;
x+4;
①當DE=DC時,
∵OA=4,OD=3, ∴DA=5, ∴![]() (0,4);
(0,4);
②過E點作EG⊥x軸于G點,
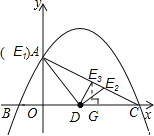
當DE=EC時,由DG=![]() ,
,
把x=OD+DG=3+![]() =
=![]() 代入到y=-
代入到y=-![]() x+4,求出y=
x+4,求出y=![]()
可得![]() ;
;
③當DC=EC時,如圖,過點E作EG⊥CD, 則△CEG∽△CAO,
∴![]() ,又OA=4,OC=8,則AC=4
,又OA=4,OC=8,則AC=4![]() ,DC=EC=5, ∴EG=
,DC=EC=5, ∴EG=![]() ,CG=2
,CG=2![]() ,
,
∴![]() (8-2
(8-2![]() ,
,![]() );
);
綜上所述,符合條件的E點共有三個:![]() (0,4)、
(0,4)、![]() 、
、![]() (8-2
(8-2![]() ,
,![]() )
)
(3)、如圖,過P作PH⊥OC,垂足為H,交直線AC與點Q;
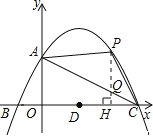
設P(m,-![]()
![]() +
+![]() m+4),則Q(m,-
m+4),則Q(m,-![]() m+4).
m+4).
①當0<m<8時,
PQ=(-![]()
![]() +
+![]() m+4)-(-
m+4)-(-![]() m+4)=-
m+4)=-![]()
![]() +2m,
+2m,
S=![]() +
+![]() =
=![]() ×8×(-
×8×(-![]()
![]() +2m)=-
+2m)=-![]() +16, ∴0<S≤16;
+16, ∴0<S≤16;
②當-2≤m<0時,
PQ=(-![]() m+4)-(-
m+4)-(-![]()
![]() +
+![]() m+4)=
m+4)=![]()
![]() -2m,
-2m,
S=![]() -
-![]() =
=![]() ×8×(
×8×(![]()
![]() -2m)=
-2m)=![]() -16,
-16,
∴0<S<20;
∴當0<S<16時,0<m<8中有m兩個值,-2<m<0中m有一個值,此時有三個;
當16<S<20時,-2<m<0中m只有一個值;
當S=16時,m=4或m=4-4![]() 這兩個. 故當S=16時,相應的點P有且只有兩個
這兩個. 故當S=16時,相應的點P有且只有兩個


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案 口算與應用題卡系列答案
口算與應用題卡系列答案 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c(a,b,c為常數,且a≠0)中的x與y的部分對應值如下表:

下列結論:
(1)ac<0; (2)當x>1時,y的值隨x值的增大而減小.
(3)3是方程ax2+(b-1)x+c=0的一個根;(4)當-1<x<3時,ax2+(b-1)x+c>0.
其中正確的的是_________;(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:
關于三角函數還有如下的公式:
Sin(α![]() β)=sinαcosβ
β)=sinαcosβ![]() cosαsinβ
cosαsinβ
tan(α![]() β)=
β)=![]()
利用這些公式可以將一些不是特殊角的三角函數轉化為特殊角的三角函數來求值,
例:tan15°=tan(45°-30°)
=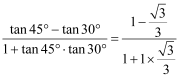
=![]()
=![]()
根據以上閱讀材料,請選擇適當的公式解答下面的問題
(1)計算sin15°
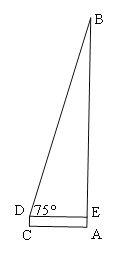
(2)我縣體育場有一移動公司的信號塔,小明想利用所學的數學知識來測量該塔的高度,小華站在離塔底A距離7米的C處,測得塔頂的仰角為75°,小華的眼睛離地面的距離DC為1.62米,請幫助小華求出該信號塔的高度。(精確到0.1米,參考數據:![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在RT△ABC中,∠ACB=90°,以AC為直徑作⊙O交AB于點D,連接CD.

(1)求證:∠DCB=∠A;
(2)若M為線段BC上一點,試問點M在什么位置時,直線DM與⊙O相切?并說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
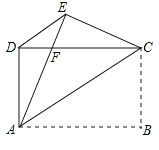
【題目】如圖,矩形ABCD中,AB=4,AD=3,把矩形沿直線AC折疊,使點B落在點E處,AE交CD于點F,連接DE.
(1)求證:△DEC≌△EDA;(2)求DF的值;(3)在線段AB上找一點P,連結FP使FP⊥AC,連結PC,試判定四邊形APCF的形狀,并說明理由,直接寫出此時線段PF的大小
查看答案和解析>>
科目:初中數學 來源: 題型:
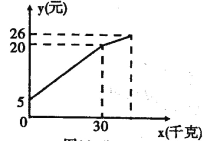
【題目】一農民帶了若干千克自產的土豆進城出售,為了方便,他帶了一些零錢備用,按市場價售出一些后,又降價出售.售出土豆千克數與他手中持有的錢數(含備用零錢)的關系如圖所示,
結合圖象回答下列問題:(1)農民自帶的零錢是多少?(2)降價前他每千克土豆出售的價格是多少?(3)降價后他按每千克0.4元將剩余土豆售完,這時他手中的錢(含備用零錢)是26元,問他一共帶了多少千克土豆?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】星光櫥具店購進電飯煲和電壓鍋兩種電器進行銷售,其進價與售價如表:
進價(元/臺) | 售價(元/臺) | |
電飯煲 | 200 | 250 |
電壓鍋 | 160 | 200 |
(1)一季度,櫥具店購進這兩種電器共30臺,用去了5600元,并且全部售完,問櫥具店在該買賣中賺了多少錢?
(2)為了滿足市場需求,二季度櫥具店決定用不超過9000元的資金采購電飯煲和電壓鍋共50臺,且電飯煲的數量不少于電壓鍋的![]() ,問櫥具店有哪幾種進貨方案?并說明理由;
,問櫥具店有哪幾種進貨方案?并說明理由;
(3)在(2)的條件下,請你通過計算判斷,哪種進貨方案櫥具店賺錢最多?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com