分析:(1)根據⊙O
1和⊙O
2是等圓,再由半徑相等,可得AO
1=O
1B=BO
2=O
2A,繼而得出四邊形AO
1BO
2是菱形;
(2)根據(1)的結論,可得∠O
1AB=∠O
2AB,由切線及圓周角定理可得∠ACE=∠AO
2C=90°,從而判斷△ACE∽△AO
2D,再由相似三角形的對應邊成比例,可得出結論;
(3)根據AC∥BO
2,可判斷△ACD∽△BO
2D,從而得出
=
=
,AD=2BD,再由高相等的兩三角形的面積之比等于底邊之比,可得出△O
2DB的面積.
解答:證明:(1)∵⊙O
1與⊙O
2是等圓,
∴AO
1=O
1B=BO
2=O
2A,
∴四邊形AO
1BO
2是菱形.
(2)∵四邊形AO
1BO
2是菱形,
∴∠O
1AB=∠O
2AB,
∵CE是⊙O
1的切線,AC是⊙O
1的直徑,
∴∠ACE=∠AO
2C=90°,
∴△ACE∽△AO
2D,
∴
=
=
,
即CE=2DO
2.
(3)∵四邊形AO
1BO
2是菱形
∴AC∥BO
2,
∴△ACD∽△BO
2D,
∴
=
=
,
∴AD=2BD,
又∵S
△AO2D=1,
∴S
△O2DB=
.
點評:本題考查了圓的綜合,涉及了圓周角定理、切線的性質、菱形的判定及相似三角形的判定與性質,綜合考察的知識點較多,解答本題需要同學具有扎實的基本功,能將所學知識融會貫通.

 (2013•梧州模擬)如圖:等圓⊙O1和⊙O2相交于A、B兩點,⊙O1經過⊙O2的圓心,順次連接A、O1、B、O2.
(2013•梧州模擬)如圖:等圓⊙O1和⊙O2相交于A、B兩點,⊙O1經過⊙O2的圓心,順次連接A、O1、B、O2.

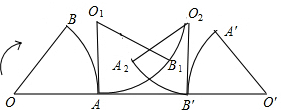 (2013•梧州模擬)如圖,已知扇形的圓心角為60°,半徑為1,將它沿著箭頭方向無滑動滾動到O′A′B′位置,則有:
(2013•梧州模擬)如圖,已知扇形的圓心角為60°,半徑為1,將它沿著箭頭方向無滑動滾動到O′A′B′位置,則有:

