
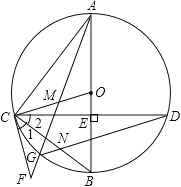
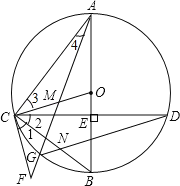
【題目】如圖,在⊙O中,直徑AB⊥CD,垂足為E,點M在OC上,AM的延長線交⊙O于點G,交過C的直線于F,∠1=∠2,連結CB與DG交于點N.
(1)求證:CF是⊙O的切線;
(2)求證:△ACM∽△DCN;
(3)若點M是CO的中點,⊙O的半徑為4,cos∠BOC=![]() ,求BN的長.
,求BN的長.
【答案】(1)證明見解析;(2)證明見解析;(3)BN=![]() .
.
【解析】試題分析:(1)、根據BO=CO得出∠B=∠BCO,根據∠2+∠B=90°,∠1=∠2得出∠1+∠BCO=90°,從而得到切線;(2)、根據AB為直徑得到∠ACB=∠FCO=90°,從而得出∠3=∠1,即∠3=∠2,結合∠4=∠D得出三角形相似;(3)、根據題意得出BE和AE的長度,然后根據勾股定理得出CE、AC和BC的長度,最后根據△ACM∽△DCN得出CN的長度,從而根據BN=BC-CN得出答案.
試題解析:(1)、∵△BCO中,BO=CO, ∴∠B=∠BCO,
在△BCE中,∠2+∠B=90°, 又∵∠1=∠2, ∴∠1+∠BCO=90°, 即∠FCO=90°,
∴CF是⊙O的切線;
(2)∵AB是⊙O直徑, ∴∠ACB=∠FCO=90°, ∴∠ACB﹣∠BCO=∠FCO﹣∠BCO,
即∠3=∠1, ∴∠3=∠2,∵∠4=∠D, ∴△ACM∽△DCN;
(3)∵⊙O的半徑為4,即AO=CO=BO=4, 在△COE中,∠BOC=![]() ,
,
∴OE=CO∠BOC=4×=1,
由此可得:BE=3,AE=5,由勾股定理可得:CE=![]() =
=![]() =
=![]() ,
,
AC=![]() =
=![]() =2
=2![]() , BC=
, BC=![]() =
=![]() =2
=2![]() ,
,
∵AB是⊙O直徑,AB⊥CD, ∴由垂徑定理得:CD=2CE=2![]() ,
,
∵△ACM∽△DCN, ∴![]() =
=![]() , ∵點M是CO的中點,CM=AO=×4=2,
, ∵點M是CO的中點,CM=AO=×4=2,
∴CN=![]() =
=![]() =
=![]() , ∴BN=BC﹣CN=2
, ∴BN=BC﹣CN=2![]() ﹣
﹣![]() =
=![]() .
.


 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:初中數學 來源: 題型:
【題目】探究題: ![]() =3,
=3, ![]() =0.5,
=0.5, ![]() =6,
=6, ![]() =
= ![]() ,
, ![]() =0.
=0.
根據以上算式,回答:
(1)![]() 一定等于a嗎?如果不是,那么
一定等于a嗎?如果不是,那么 ![]() =;
=;
(2)利用你總結的規律,計算: ①若x<2,則 ![]() =;
=;
② ![]() = .
= .
(3)若a,b,c為三角形的三邊長,化簡: ![]() +
+ ![]() +
+ ![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】把一張長方形紙片ABCD沿EF折疊后ED與BC的交點為G,D、C分別在M、N的位置上,若∠EFG=55°,求:
(1)∠FED的度數;
(2)∠FEG的度數;
(3)∠1和∠2的度數.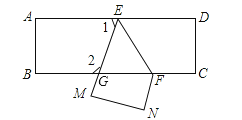
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在□ABCD中,∠B=100°,則∠A,∠D的度數分別是( )
A. ∠A=80°,∠D=80° B. ∠A=80°,∠D=100°
C. ∠A=100°,∠D=80° D. ∠A=100°,∠D=100°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖過刨平的木板上的兩個點,能彈出一條筆直的墨線,而且只能彈出一條墨線,能解釋這一實際應用的數學知識是( ) 
A.兩點確定一條直線
B.兩點之間線段最短
C.垂線段最短
D.在同一平面內,過一點有且只有一條直線與已知直線垂直
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司全體職工的月工資如下:
月工資(元) | 18000 | 12000 | 8000 | 6000 | 4000 | 2500 | 2000 | 1500 | 1200 |
人數 | 1(總經理) | 2(副總經理) | 3 | 4 | 10 | 20 | 22 | 12 | 6 |
該公司月工資數據的眾數為2000,中位數為2250,平均數為3115,極差為16800,公司的普通員工最關注的數據是( )
A. 中位數和眾數B. 平均數和眾數
C. 平均數和中位數D. 平均數和極差
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com