
【題目】如圖1,在平整的地面上,用![]() 個棱長都為
個棱長都為![]() 的小正方體堆成一個幾何體.
的小正方體堆成一個幾何體.
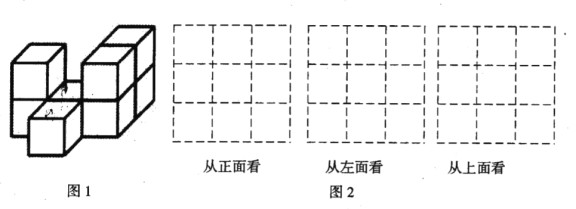
![]() 請在圖2中畫出從正面、左面和上面看到的這個幾何體的形狀圖;
請在圖2中畫出從正面、左面和上面看到的這個幾何體的形狀圖;
![]() 如果現在你還有一些大小相同的小正方體,要求保持從上面和左面看到的形狀圖都不變,最多可以再添加 個小正方體;
如果現在你還有一些大小相同的小正方體,要求保持從上面和左面看到的形狀圖都不變,最多可以再添加 個小正方體;
![]() 圖1中
圖1中![]() 個小正方體搭成的幾何體的表面積(包括與地面接觸的部分)是
個小正方體搭成的幾何體的表面積(包括與地面接觸的部分)是 ![]()
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】在前面的學習中,我們通過對同一面積的不同表達和比較,根據圖①和圖②發現并驗證了平方差公式和完全平方公式.這種利用面積關系解決問題的方法,使抽象的數量關系因幾何直觀而形象化.
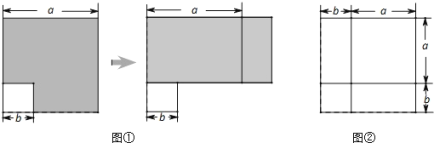
請你利用上述方法解決下列問題:
(1)請寫出圖1和圖2所表示的代數恒等式
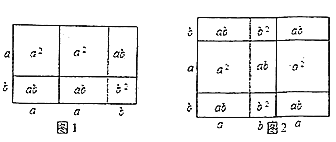
_______ _______
(2)現有a×a,b×b的正方形紙片和a×b的矩形紙片各若干塊,試選用這些紙片(每種紙片至少用一次,每兩個紙片之間既不重疊,也無空隙,拼出的圖形中必須保留拼圖的痕跡),使拼出的矩形面積為為2a2+5ab+2b2,并標出此矩形的長和寬.
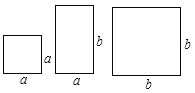
(拓展應用)
提出問題:47×43,56×54,79×71,…是一些十位數字相同,且個位數字之和是10的兩個兩位數相乘的算式,是否可以找到一種速算方法?
幾何建模:用矩形的面積表示兩個正數的乘積,以47×43為例:
(1)畫長為47,寬為43的矩形,如圖③,將這個47×43的矩形從右邊切下長40,寬3的一條,拼接到原矩形上面.
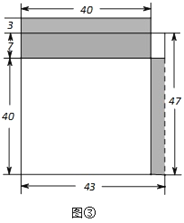
(2)原矩形面積可以有兩種不同的表達方式:47×43的矩形面積或(40+7+3)×40的矩形與右上角3×7的矩形面積之和,47×43=(40+10)×40+3×7=5×4×100+3×7=2021,
用文字表述47×43的速算方法是:十位數字4加1的和與4相乘,再乘以100,加上個位數字3與7的積,構成運算結果.
歸納提煉:
兩個十位數字相同,并且個位數字之和是10的兩位數相乘的速算方法是(用文字表述)_________.
證明上述速算方法的正確性;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知![]() ,
,![]() 兩點在數軸上,點
兩點在數軸上,點![]() 表示的數為-10,點
表示的數為-10,點![]() 到點
到點![]() 的距離是點
的距離是點![]() 到點
到點![]() 距離的3倍,點
距離的3倍,點![]() 以每秒3個單位長度的速度從點
以每秒3個單位長度的速度從點![]() 向右運動.點
向右運動.點![]() 以每秒2個單位長度的速度從點
以每秒2個單位長度的速度從點![]() 向右運動(點
向右運動(點![]() 、
、![]() 同時出發)
同時出發)
![]()
(1)數軸上點![]() 對應的數是______.
對應的數是______.
(2)經過幾秒,點![]() 、點
、點![]() 分別到原點
分別到原點![]() 的距離相等.
的距離相等.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線y1=x2-2x-3與x軸相交于點A,B(點A在B的左側),與y軸相交于點C,直線y2=kx+b經過點B,C.
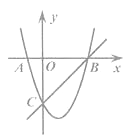
(1)求直線BC的函數關系式;
(2)當y1>y2時,請直接寫出x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,AD∥BC,AD=5,B(-3,0),C(9,0),點E是BC的中點,點P是線段BC上一動點,當PB=________時,以點P、A、D、E為頂點的四邊形是平行四邊形.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】解答下列問題:
![]() 畫出數軸,并在數軸上表示
畫出數軸,并在數軸上表示![]() 與
與![]() ;
;
![]() 數軸上表示
數軸上表示![]() 的點與表示
的點與表示![]() 的兩點之間的距離為 ;
的兩點之間的距離為 ;
![]() 若
若![]() ,且點
,且點![]() ,點
,點![]() 在數軸上表示的數分別是
在數軸上表示的數分別是![]() ,則
,則![]() 兩點間的最大距離 ,最小距離是
兩點間的最大距離 ,最小距離是
![]() 數軸上
數軸上![]() 的三點所表示的數分別為
的三點所表示的數分別為![]() .點
.點![]() 在點
在點![]() 左側,點
左側,點![]() 與點
與點![]() 之間的距離為
之間的距離為![]() ,點
,點![]() 與點
與點![]() 之間的距離為
之間的距離為![]() ,如果
,如果![]() 兩點同時出發,點
兩點同時出發,點![]() 以每分鐘
以每分鐘![]() 個單位長度的速度從點
個單位長度的速度從點![]() 向右運動,點
向右運動,點![]() 以每分鐘
以每分鐘![]() 個單位長度從點
個單位長度從點![]() 向左運動.
向左運動.
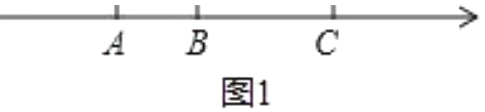
①如圖1, 分鐘后,點![]() 與點
與點![]() 的距離和點
的距離和點![]() 與點
與點![]() 的距離相等;
的距離相等;
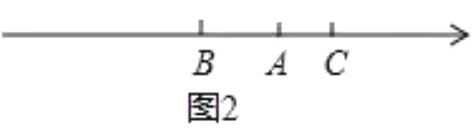
②如圖2, 分鐘后,點 ![]() 與點
與點![]() 的距離和點
的距離和點![]() 與點
與點![]() 的距離相等.
的距離相等.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為打造書香校園,計劃購進甲乙兩種規格的書柜放置新購置的圖書,調查發現,若購買甲種書柜3個,乙種書柜2個,共需要資金1020元;若購買甲種書柜4個,乙種書柜3個,共需資金1440元.
(1)甲乙兩種書柜每個的價格分別是多少元?
(2)若該校計劃購進這兩種規格的書柜共20個(其中乙種書柜的數量不少于甲種書柜的數量的![]() ).設該校計劃購進甲種書柜m個,資金總額為W元.求W與m的函數關系式,并請你為該校設計資金最少的購買方案.
).設該校計劃購進甲種書柜m個,資金總額為W元.求W與m的函數關系式,并請你為該校設計資金最少的購買方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某慈善組織租用甲、乙兩種貨車共![]() 輛,把蔬菜
輛,把蔬菜![]() 噸,水果
噸,水果![]() 噸,全部運到災區已知輛甲種貨車同時可裝蔬菜
噸,全部運到災區已知輛甲種貨車同時可裝蔬菜![]() 噸,水果
噸,水果![]() 噸;一輛乙種貨車同時可裝蔬菜
噸;一輛乙種貨車同時可裝蔬菜![]() 噸,水果
噸,水果![]() 噸.
噸.
(1)若將這批貨物一次性運到災區,請寫出具體的租車方案?
(2)若甲種貨車每輛需付燃油費![]() 元,乙種貨車每輛需付燃油費
元,乙種貨車每輛需付燃油費![]() 元,則應選(1)種的哪種方案,才能使所付的燃油費最少?最少的燃油費是多少元?
元,則應選(1)種的哪種方案,才能使所付的燃油費最少?最少的燃油費是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,AB=6,點E在邊CD上,且DE=2.將△ADE沿AE對折得到△AFE,延長EF交邊BC于點G,則BG=___________.
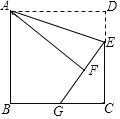
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com