
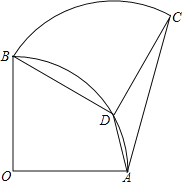
【題目】如圖,扇形OAB中,∠AOB=90°,將扇形OAB繞點B逆時針旋轉,得到扇形BDC,若點O剛好落在弧AB上的點D處,則![]() 的值為( )
的值為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
如圖,連OD、AB、BC,延長AD交BC于H點,由旋轉的性質可得BD=BO=OD=CD=OA,∠BDC=90°,可證△ABC是等邊三角形,由線段垂直平分線的性質可得AH垂直平分BC,由等腰直角三角形的性質和等邊三角形的性質可得AC=2CH,AD=![]() CH-CH,即可求解.
CH-CH,即可求解.
解:如圖,連OD、AB、BC,延長AD交BC于H點,
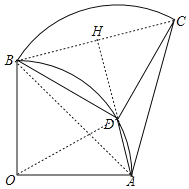
∵將扇形OAB繞點B逆時針旋轉,得到扇形BDC,若點O剛好落在弧AB上的點D處,
∴BD=BO=OD=CD=OA,∠BDC=90°
∴∠OBD=60°,即旋轉角為60°,
∴∠ABC=60°,又可知AB=BC,
∴△ABC是等邊三角形,
∵AB=AC,BD=CD,
∴AH垂直平分BC,
∴∠CAH=30°,
∴AC=2CH,AH=![]() CH,
CH,
∵BD=CD,∠BDC=90°,DH⊥BC,
∴DH=CH,
∴AD=![]() CH﹣CH,
CH﹣CH,
∴![]() =
=![]() .
.
故選:A.


科目:初中數學 來源: 題型:
【題目】抗擊新冠肺炎期間,某小區為方便管理,為居民設計了一個身份識別圖案系統:在4×4的正方形網格中,白色正方形表示數字1,黑色正方形表示數字0,將第i行第j列表示的數記為ai,j(其中i,j都是不大于4的正整數),例如,圖1中,a1,2=0.對第i行使用公式Ai=ai,1×23+ai,2×22+ai,3×21+ai,4×20進行計算,所得結果A1,A2,A3,A4分別表示居民樓號,單元號,樓層和房間號.例如,圖1中,A3=a3,1×23+a3,2×22+a3,3×21+a3,4×20=1×8+0×4+0×2+1×1=9,A4=0×8+0×4+1×2+1×1=3,說明該居民住在9層,3號房間,即903號.
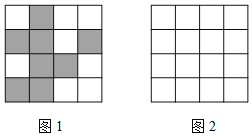
(1)圖1中,a1,3= ;
(2)圖1代表的居民居住在 號樓 單元;
(3)請仿照圖1,在圖2中畫出8號樓4單元602號居民的身份識別圖案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩家商場平時以同樣的價格出售相同的商品.“五一”節期間兩家商場都讓利酬賓.在甲商場按累計購物金額的![]() 收費;在乙商場累計購物金額超過
收費;在乙商場累計購物金額超過![]() 元后,超出
元后,超出![]() 元的部分按
元的部分按![]() 收費.設小紅在同一商場累計購物金額為
收費.設小紅在同一商場累計購物金額為![]() 元,其中
元,其中![]() .
.
(1)根據題意,填寫下表(單位:元):
累計購物金額 |
|
|
| ··· |
在甲商場實際花費 |
| ··· | ||
在乙商場實際花費 |
| ··· |
(2)設小紅在甲商場實際花費![]() 元,在乙商場實際花費
元,在乙商場實際花費![]() 元,分別求
元,分別求![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(3)“五一”節期間小紅如何選擇這兩家商場去購物更省錢?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某景區為了解游客人數的變化規律,提高旅游服務質量,收集并整理了某月(30天)接待游客人數(單位:萬人)的數據,繪制了下面的統計圖和統計表:
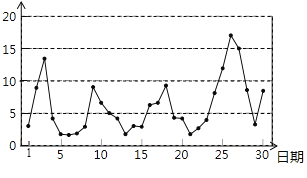
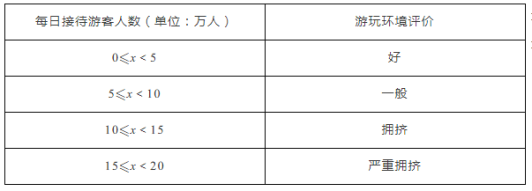
根據以上信息,以下四個判斷中,正確的是_________.(填寫所有正確結論的序號)
①該景區這個月游玩環境評價為“擁擠或嚴重擁擠”的天數僅有4天;
②該景區這個月每日接待游客人數的中位數在5~10廣域網人之間;
③該景區這個月平均每日接待游客人數低于5萬人;
④這個月1日至5日的五天中,如果某人曾經隨機選擇其中的兩天到該景區游玩,那么他“這兩天游玩環境評價均為好”的可能性為![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=ax2+bx+a+2(a≠0)與x軸交于點A(x1,0),點B(x2,0),(點A在點B的左側),拋物線的對稱軸為直線x=-1.
(1)若點A的坐標為(-3,0),求拋物線的表達式及點B的坐標;
(2)C是第三象限的點,且點C的橫坐標為-2,若拋物線恰好經過點C,直接寫出x2的取值范圍;
(3)拋物線的對稱軸與x軸交于點D,點P在拋物線上,且∠DOP=45°,若拋物線上滿足條件的點P恰有4個,結合圖象,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,對角線AC、BD相交于點O,過點D作對角線BD的垂線交BA的延長線于點E.
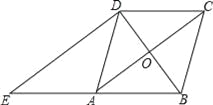
(1)證明:四邊形ACDE是平行四邊形;
(2)若AC=8,BD=6,求△ADE的周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校在開展讀書交流活動中,全體師生積極捐書,為了解所捐書籍的種類,對部分書籍進行了抽樣調查,張老師根據調查數據繪制了如下不完整的統計圖.
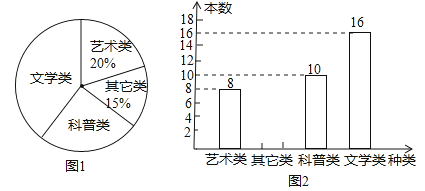
請根據統計圖回答下列問題:
(1)本次抽樣調查的書籍有多少本?
(2)試求圖1中表示文學類書籍的扇形圓心角的度數,并補全條形統計圖.
(3)本次活動師生共捐書![]() 本,請估計有多少本科普類書籍?
本,請估計有多少本科普類書籍?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知銳角∠AOB,如圖,(1)在射線OA上取一點C,以點O為圓心,OC長為半徑作![]() ,交射線OB于點D,連接CD;(2)分別以點C,D為圓心,CD長為半徑作弧,兩弧交于點P,連接CP,DP;(3)作射線OP交CD于點Q.根據以上作圖過程及所作圖形,下列結論中錯誤的是( )
,交射線OB于點D,連接CD;(2)分別以點C,D為圓心,CD長為半徑作弧,兩弧交于點P,連接CP,DP;(3)作射線OP交CD于點Q.根據以上作圖過程及所作圖形,下列結論中錯誤的是( )
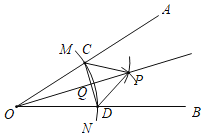
A.CP∥OBB.CP=2QCC.∠AOP=∠BOPD.CD⊥OP
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com