
【題目】在矩形![]() 中,已知
中,已知![]() ,在邊
,在邊![]() 上取點
上取點![]() ,使
,使![]() ,連結
,連結![]() ,過點
,過點![]() 作
作![]() ,與邊
,與邊![]() 或其延長線交于點
或其延長線交于點![]() .
.
猜想:如圖①,當點![]() 在邊
在邊![]() 上時,線段
上時,線段![]() 與
與![]() 的大小關系為 .
的大小關系為 .
探究:如圖②,當點![]() 在邊
在邊![]() 的延長線上時,
的延長線上時,![]() 與邊
與邊![]() 交于點
交于點![]() .判斷線段
.判斷線段![]() 與
與![]() 的大小關系,并加以證明.
的大小關系,并加以證明.
應用:如圖②,若![]() 利用探究得到的結論,求線段
利用探究得到的結論,求線段![]() 的長.
的長.

【答案】猜想:AF=DE;探究:AF=DE;應用:BG=![]()
【解析】
試題分析:先猜想,再根據垂直的意義和矩形的性質證明△AEF≌△DCE即可說明AF=DE;然后可根據圖形結合題意可求得AF=3,BF=1,然后用平行線的性質,證明△FBG∽△FAE,再根據相似三角形的對應邊成比例求得結果.
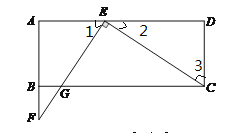
試題解析:猜想:AF=DE
探究:AF=DE
證明:∵EF⊥CE
∴∠CEF=90°
∴∠1+∠2=90°
∵四邊形ABCD為矩形
∴∠A=∠D=90°,AB=CD
∴∠2+∠3=90°
∴∠1=∠3
∵AE=AB,
∴AE=DC
∴△AEF≌△DCE
∴AF=DE
應用:∵AF=DE=AD-AE=5-2=3
∴BF=AF-AB=3-2=1
在矩形ABCD中,AD∥BC
∴△FBG∽△FAE
∴![]()
即![]()
∴BG=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】元旦期間,某超市銷售兩種不同品牌的蘋果,已知1千克甲種蘋果和1千克乙種蘋果的進價之和為18元.當銷售1千克甲種蘋果和1千克乙種蘋果利潤分別為4元和2元時,陳老師購買3千克甲種蘋果和4千克乙種蘋果共用82元.
(1)求甲、乙兩種蘋果的進價分別是每千克多少元?
(2)在(1)的情況下,超市平均每天可售出甲種蘋果100千克和乙種蘋果140千克,若將這兩種蘋果的售價各提高1元,則超市每天這兩種蘋果均少售出10千克,超市決定把這兩種蘋果的售價提高x元,在不考慮其他因素的條件下,使超市銷售這兩種蘋果共獲利960元,求x的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某廠家生產一種新型電子產品,制造時每件的成本為40元,通過試銷發現,銷售量![]() 萬件
萬件![]() 與銷售單價
與銷售單價![]() 元
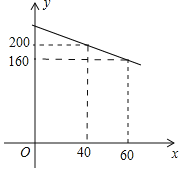
元![]() 之間符合一次函數關系,其圖象如圖所示.
之間符合一次函數關系,其圖象如圖所示.
![]() 求y與x的函數關系式;
求y與x的函數關系式;
![]() 物價部門規定:這種電子產品銷售單價不得超過每件80元,那么,當銷售單價x定為每件多少元時,廠家每月獲得的利潤
物價部門規定:這種電子產品銷售單價不得超過每件80元,那么,當銷售單價x定為每件多少元時,廠家每月獲得的利潤![]() 最大?最大利潤是多少?
最大?最大利潤是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
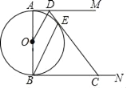
【題目】如圖,⊙O的直徑AB=6,AM,BN是⊙O的兩條切線,點D是AM上一點,連接OD,作BE∥OD交⊙O于點E,連接DE并延長交BN于點.
(1)求證:DC是⊙O的切線;
(2)設AD=x,BC=y.求y與x的函數關系式(不要求寫出自變量的取值范圍)
(3)若AD=1,連接AE并延長交BC于F,求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
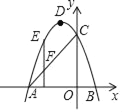
【題目】如圖,在直角坐標系中,拋物線y=﹣(x+1)2+4與x軸交于點A、B,與y軸交于點C.
(1)寫出拋物線頂點D的坐標 ;
(2)點D1是點D關于y軸的對稱點,判斷點D1是否在直線AC上,并說明理由;
(3)若點E是拋物線上的點,且在直線AC的上方,過點E作EF⊥x軸交線段AC于點F,求線段EF的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
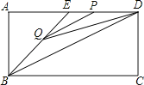
【題目】如圖,在矩形ABCD中,AB=2,點E在邊AD上,∠ABE=45°,BE=DE,連接BD,點P在線段DE上,過點P作PQ∥BD交BE于點Q,連接QD.設PD=x,△PQD的面積為y,則能表示y與x函數關系的圖象大致是( )

查看答案和解析>>
科目:初中數學 來源: 題型:
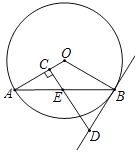
【題目】如圖,AB是⊙O的弦,過AB的中點E作EC⊥OA,垂足為C,過點B作直線BD交CE的延長線于點D,使得DB=DE.
(1)求證:BD是⊙O的切線;
(2)若AB=12,DB=5,求△AOB的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個口袋中有4個完全相同的小球,把它們分別標上數字﹣1,0,1,2,隨機的摸出一個小球記錄數字然后放回,在隨機的摸出一個小球記錄數字.求下列事件的概率:
(1)兩次都是正數的概率P(A);
(2)兩次的數字和等于0的概率P(B).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB是⊙O的直徑,過點B作⊙O的切線BM,弦CD//BM,交AB于點F,且![]() ,連接AC,AD,延長AD交BM于點E.
,連接AC,AD,延長AD交BM于點E.
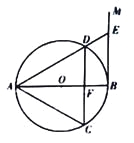
(l)求證:△ACD是等邊三角形;
(2)連接OE,若DE=2,求OE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com