
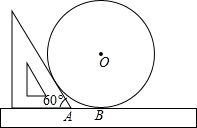
 如圖,直尺、三角尺都和圓O相切,AB=8cm.求圓O的直徑.
如圖,直尺、三角尺都和圓O相切,AB=8cm.求圓O的直徑.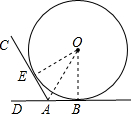 連接OE、OA、OB,
連接OE、OA、OB, ∠BAC,
∠BAC, ×120°=60°,
×120°=60°, =
=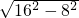 =8
=8 (cm),
(cm), cm,
cm, cm,
cm, cm.
cm. ∠BAC,求出∠BAC,求出∠OAB和∠BOA,求出OA,根據勾股定理求出OB即可.
∠BAC,求出∠BAC,求出∠OAB和∠BOA,求出OA,根據勾股定理求出OB即可.

 名校練考卷期末沖刺卷系列答案
名校練考卷期末沖刺卷系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com