
【題目】如圖,已知點A的坐標為(4,0),點B的坐標為(0,3),在第一象限內找一點P(a,b) ,使△PAB為等邊三角形,則2(a-b)=___________.

【答案】![]()
【解析】
根據A、B坐標求出直線AB的解析式后,求得AB中點M的坐標,連接PM,在等邊△PAB中,M為AB中點,所以PM⊥AB,![]() ,再求出直線PM的解析式,求出點P坐標;在Rt△PAM中,AP=AB=5,
,再求出直線PM的解析式,求出點P坐標;在Rt△PAM中,AP=AB=5,![]() ,即
,即![]() 且a>0,解得a>0,即
且a>0,解得a>0,即![]() ,將a代入直線PM的解析式中求出b的值,最后計算2(a-b)的值即可;
,將a代入直線PM的解析式中求出b的值,最后計算2(a-b)的值即可;
解:∵A(4,0),B(0,3),
∴AB=5,
設![]() ,
,
∴![]() ,
,
∴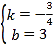 ,
,
∴![]() ,
,
∵A(4,0) B(0,3) ,
∴AB中點![]() ,連接PM,
,連接PM,
在等邊△PAB中,M為AB中點,
∴PM⊥AB,![]() ,
,
∴![]() ,
,
∴設直線PM的解析式為![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
在Rt△PAM中,AP=AB=5,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵a>0,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,點![]() 在直線
在直線![]() 上,點
上,點![]() 的橫坐標為
的橫坐標為![]() ,過
,過![]() 作
作![]() ,交
,交![]() 軸于點
軸于點![]() ,以
,以![]() 為邊,向右作正方形
為邊,向右作正方形![]() ,延長
,延長![]() 交
交![]() 軸于點
軸于點![]() ;以
;以![]() 為邊,向右作正方形
為邊,向右作正方形![]() ,延長
,延長![]() 交
交![]() 軸于點
軸于點![]() ;以
;以![]() 為邊,向右作正方形
為邊,向右作正方形![]() 延長
延長![]() 交
交![]() 軸于點
軸于點![]() ;按照這個規律進行下去,點
;按照這個規律進行下去,點![]() 的橫坐標為_____(結果用含正整數
的橫坐標為_____(結果用含正整數![]() 的代數式表示)
的代數式表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=x2﹣2ax+m.
(1)當a=2,m=﹣5時,求拋物線的最值;
(2)當a=2時,若該拋物線與坐標軸有兩個交點,把它沿y軸向上平移k個單位長度后,得到新的拋物線與x軸沒有交點,請判斷k的取值情況,并說明理由;
(3)當m=0時,平行于y軸的直線l分別與直線y=x﹣(a﹣1)和該拋物線交于P,Q兩點.若平移直線l,可以使點P,Q都在x軸的下方,求a的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
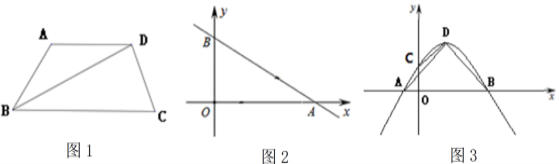
【題目】有一組鄰邊相等的凸四邊形叫做“和睦四邊形”,寓意是全世界和平共處,睦鄰友好,共同發展.如菱形,正方形等都是“和睦四邊形”.
(1)如圖1,BD平分∠ABC,AD∥BC,求證:四邊形ABCD為“和睦四邊形”;
(2)如圖2,直線![]() 與x軸、y軸分別交于A、B兩點,點P、Q分別是線段OA、AB上的動點.點P從點A出發,以每秒4個單位長度的速度向點O運動.點Q從點A出發,以每秒5個單位長度的速度向點B運動.P、Q兩點同時出發,設運動時間為t秒.當四邊形BOPQ為“和睦四邊形”時,求t的值;
與x軸、y軸分別交于A、B兩點,點P、Q分別是線段OA、AB上的動點.點P從點A出發,以每秒4個單位長度的速度向點O運動.點Q從點A出發,以每秒5個單位長度的速度向點B運動.P、Q兩點同時出發,設運動時間為t秒.當四邊形BOPQ為“和睦四邊形”時,求t的值;
(3)如圖3,拋物線![]() 與
與![]() 軸交于A、B兩點(點A在點B的左側),與y軸交于點
軸交于A、B兩點(點A在點B的左側),與y軸交于點![]() ,拋物線的頂點為點D.當四邊形COBD為“和睦四邊形”,且CD=OC.拋物線還滿足:①
,拋物線的頂點為點D.當四邊形COBD為“和睦四邊形”,且CD=OC.拋物線還滿足:①![]() ;②頂點D在以AB為直徑的圓上. 點
;②頂點D在以AB為直徑的圓上. 點![]() 是拋物線
是拋物線![]() 上任意一點,且
上任意一點,且![]() .若
.若![]() 恒成立,求m的最小值.
恒成立,求m的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
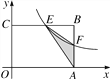
【題目】如圖,在矩形OABC中,OA=3,OC=2,F是AB上的一個動點(F不與A,B重合),過點F的反比例函數y=![]() (x>0)的圖象與BC邊交于點E.
(x>0)的圖象與BC邊交于點E.
(1)當F為AB的中點時,求該函數的解析式;
(2)當k為何值時,△EFA的面積最大,最大面積是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】歡歡放學回家看到桌上有三個禮包,是爸爸送給歡歡和姐姐的禮物,其中![]() 禮包是芭比娃娃,
禮包是芭比娃娃,![]() 和
和![]() 禮包都是智能對話機器人.這些禮包用外表一樣的包裝盒裝著,看不到里面的禮物.
禮包都是智能對話機器人.這些禮包用外表一樣的包裝盒裝著,看不到里面的禮物.
(1)歡歡隨機地從桌上取出一個禮包,取出的是芭比娃娃的概率是多少?
(2)請用樹狀圖或列表法表示歡歡隨機地從桌上取出兩個禮包的所有可能結果,并求取出的兩個禮包都是智能對話機器人的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊三角形ABC的邊長為5,D、E分別是邊AB、AC上的點,將△ADE沿DE折疊,點A恰好落在BC邊上的點F處,若BF=2,則BD的長是( )
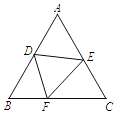
A.2B.3C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com