
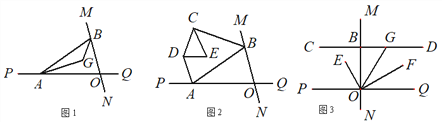
【題目】直線MN與直線PQ相交于O,點A在射線OP上,點B在射線OM上.
(1)如圖1,![]() 已知AG、BG分別是∠BAO和∠ABO角的平分線,求
已知AG、BG分別是∠BAO和∠ABO角的平分線,求![]() 的度數;
的度數;
(2)如圖2,![]() 已知AB不平行CD,AD、BC分別是∠BAP和∠ABM的角平分線,又DE、CE分別是∠ADC和∠BCD的角平分線,∠CED= 度;
已知AB不平行CD,AD、BC分別是∠BAP和∠ABM的角平分線,又DE、CE分別是∠ADC和∠BCD的角平分線,∠CED= 度;
(3)如圖3,![]() ,過點B作直線CD⊥MN,G為射線BD上一點,OF平分∠QOG,OE⊥OF,探索
,過點B作直線CD⊥MN,G為射線BD上一點,OF平分∠QOG,OE⊥OF,探索![]() 的大小是否發生變化?若不變,求其值;若改變,說明理由.
的大小是否發生變化?若不變,求其值;若改變,說明理由.
【答案】(1)![]() ;(2)50°;(3)比值為2,理由見解析.
;(2)50°;(3)比值為2,理由見解析.
【解析】分析:(1)根據三角形內角和定理,求得![]() 的度數,再利用角平分線的性質可得:
的度數,再利用角平分線的性質可得:![]() 即可求解;
即可求解;
(2)根據三角形內角和定理,求得![]() 的度數,再利用平角的定義可得:∠PAB+∠MBA=360°-(
的度數,再利用平角的定義可得:∠PAB+∠MBA=360°-(![]() ),再由角角平分線的性質可得∠DAB+∠ABC=
),再由角角平分線的性質可得∠DAB+∠ABC=![]() ,再根據三角形內角和定理即可求得∠CED的度數;
,再根據三角形內角和定理即可求得∠CED的度數;
(3)設![]() ,由平行線的性質可得:∠QOG
,由平行線的性質可得:∠QOG![]() ,再由角平分線的性質可得:∠GOF=
,再由角平分線的性質可得:∠GOF=![]() ,由OE⊥OF可得∠BOG+∠GOF=
,由OE⊥OF可得∠BOG+∠GOF=![]() ,由
,由![]() 可得∠QOF+∠BOF=
可得∠QOF+∠BOF=![]() ,則有
,則有![]() ,則
,則![]() ,則可求得它們的比值.
,則可求得它們的比值.
詳解:
(1)∵![]() ,
,
∴![]() ,
,
又∵AG、BG平分![]() 、
、![]() ,
,
∴![]() ,
,
又∵![]() +∠AGB=
+∠AGB=![]() ,
,
∴∠AGB=180![]() -50
-50![]() =130
=130![]() ;
;
(2)∵![]() ,
,
∴![]() ,
,
∴∠PAB+∠MBA=360°-(![]() )=260
)=260![]() ,
,
又∵DE、CE分別是∠ADC和∠BCD的角平分線,
∴∠DAB+∠ABC=![]() =130°,
=130°,
又∵∠DAB+∠ABC+∠DEC=180°(折疊前,這三個角是△ABE的內角)
∴∠DEC=180°-130°=50°.
(3)設![]()
∵![]()
∴CD∥PQ,
∴![]() ,
,
又∵OF平分![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴ ![]() ,
,
∴ ![]() ,
,
∴![]() ,不變化.
,不變化.


科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,則圖中的全等三角形對數共有( )
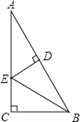
A. 1對 B. 2對 C. 3對 D. 4對
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某數學興趣小組研究我國古代《算法統宗》里這樣一首詩:我問開店李三公,眾客都來到店中,一房七客多七客,一房九客一房空.詩中后兩句的意思是:如果每一間客房住7人,那么有7人無房可住;如果每一間客房住9人,那么就空出一間房.
(1)求該店有客房多少間?房客多少人?
(2)假設店主李三公將客房進行改造后,房間數大大增加.每間客房收費20錢,且每間客房最多入住4人,一次性定客房18間以上(含18間),房費按8折優惠.若詩中“眾客”再次一起入住,他們如何訂房更合算?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我們給出如下定義:順次連接任意一個四邊形各邊中點所得的四邊形叫中點四邊形.

(1)如圖1,四邊形ABCD中,點E,F,G,H分別為邊AB,BC,CD,DA的中點.求證:中點四邊形EFGH是平行四邊形;
(2)如圖2,點P是四邊形ABCD內一點,且滿足PA=PB,PC=PD,∠APB=∠CPD,點E,F,G,H分別為邊AB,BC,CD,DA的中點,猜想中點四邊形EFGH的形狀,并證明你的猜想;
(3)若改變(2)中的條件,使∠APB=∠CPD=90°,其他條件不變,直接寫出中點四邊形EFGH的形狀.(不必證明)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,E是BC的中點,連接AE并延長交DC的延長線于點F.

(1)求證:AB=CF;
(2)連接DE,若AD=2AB,求證:DE⊥AF.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,等邊△ABC的邊長是2,D、E分別為AB、AC的中點,延長BC至點F,使CF=![]() BC,連接CD和EF.
BC,連接CD和EF.
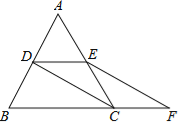
(1)求證:DE=CF;
(2)求EF的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,對角線AC,BD相交于點O,點E,F分別在OA,OC上
(1)給出以下條件;①OB=OD,②∠1=∠2,③OE=OF,請你從中選取兩個條件證明△BEO≌△DFO;
(2)在(1)條件中你所選條件的前提下,添加AE=CF,求證:四邊形ABCD是平行四邊形.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com