Question

【題目】如圖，△ABE是⊙O的內接三角形，AB為直徑，過點B的切線與AE的延長線交于點C，D是BC的中點，連接DE，連接CO，線段CO的延長線交⊙O于F，FG⊥AB于G．
（1）求證：DE是⊙O的切線；
（2）若AE=4，BE=2，求AG的長．

Answer 1

【答案】
（1）證明：連接OE，OD，

在△OED與△OBD中， ，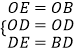

∴△OED≌△OBD，

∴∠OED=∠OBD，

∵BC是⊙O的切線，

∴∠OBD=90°，

∴∠OED=90°，

∴OE⊥ED，

∴DE是⊙O的切線；

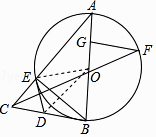
（2）解：∵AB為⊙O的直徑，

∴∠AEB=90°，

∴AB= =2 ，

∴OF=OB= ，

∵△AEB∽△BEC，

∴ ，

∴BC= = ，

∴OC= = = ，

∵∠AOF=∠BOC，

∵FG⊥AB，

∴∠FGO=90°，

∴∠FGO=∠OBC=90°，

∴△OFG∽△OBC，

∴ ，

∴OG= OB= ，

∴AG=AO﹣OG= ﹣ ．

【解析】（1）連接OE，OD，根據全等三角形的性質得到∠OED=∠OBD，由BC是⊙O的切線，得到∠OBD=90°，于是得到結論；（2）由AB為⊙O的直徑，得到∠AEB=90°，根據勾股定理得到AB= =2 ，求得OF=OB= 根據相似三角形的性質得到BC= = ，根據勾股定理到OC= = = ，根據相似三角形的性質即可得到結論．