
 已知二次函數
已知二次函數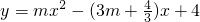 .
.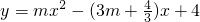 的圖象與x軸是否有交點?
的圖象與x軸是否有交點?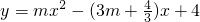 與x軸交于A、B兩點,與y軸交于點C,請求出點A、B、C的坐標(可用含m的代數式表示).
與x軸交于A、B兩點,與y軸交于點C,請求出點A、B、C的坐標(可用含m的代數式表示). )2-16m=(3m-
)2-16m=(3m- )2≥0,
)2≥0, )x+4=0,解得x=3或
)x+4=0,解得x=3或 ,
, ,0),C(0,4);
,0),C(0,4); )×(-2)+4=0,解得m=-
)×(-2)+4=0,解得m=- ,
, )×8+4=0,解得m=
)×8+4=0,解得m= ,
, )×(-3)+4=0,解得m=-
)×(-3)+4=0,解得m=- ,
, ,
, ,0),
,0), )2-(3m+
)2-(3m+ )×(-
)×(- )+4=0,解得m=-
)+4=0,解得m=- ,
, x2+
x2+ x+4或y=
x+4或y= x2-
x2- x+4或y=-
x+4或y=- x2+4或y=-
x2+4或y=- x2-+
x2-+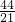 x+4.
x+4.

科目:初中數學 來源: 題型:
| A、y1≥y2 | B、y1>y2 | C、y1<y2 | D、y1≤y2 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•莒南縣二模)已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列5個結論:
(2013•莒南縣二模)已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,有下列5個結論:查看答案和解析>>
科目:初中數學 來源: 題型:
 已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則下列結論:①ac>0;②a-b+c<0;
已知二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,則下列結論:①ac>0;②a-b+c<0;查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com