
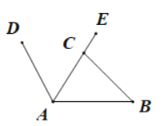
【題目】為倡導“綠色出行,低碳生活”的號召,今年春天,安慶市的街頭出現了一道道綠色的風景線--“共享單車”. 圖(1)所示的是一輛共享單車的實物圖. 圖(2)是這輛共享單車的部分幾何示意圖,其中車架檔AC長為40cm,座桿CE的長為18cm. 點A、C、E在同一條直線上,且∠CAB=60°,∠ACB=75°
(1)求車座點E到車架檔AB的距離;
(2)求車架檔AB的長.

【答案】(1)車座點E到車架檔AB的距離為![]() ;(2)車架檔AB的長為
;(2)車架檔AB的長為![]()
【解析】
(1)過E作EF⊥AB,垂足為F,運用EF=AE·sin∠CAB=58sin60°可得;
(2)過C作CG⊥AB,垂足為G,可得AG=AC·cos∠CAB=40cos60°,CG=AC·sin∠CAB=40sin60°,在Rt△BCG中,則BG=CG=![]() cm,故AB=AG+BG.
cm,故AB=AG+BG.
解(1)過E作EF⊥AB,垂足為F.
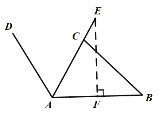
AE=AC+CE=58cm
在Rt△AEF中,∠CAB=60°,AE=58cm,
∴EF=AE·sin∠CAB=58sin60°=![]() cm.
cm.
答:車座點E到車架檔AB的距離為![]()
(2)過C作CG⊥AB,垂足為G,
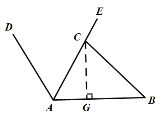
在Rt△ACG中,∠CAB=60°,AC=40cm,
則∠ACG=30°,∠BCG=∠ACB-∠ACG=45°
AG=AC·cos∠CAB=40cos60°=20cm
CG=AC·sin∠CAB=40sin60°=![]() cm
cm
在Rt△BCG中,∠BCG=45°,CG=![]() cm
cm
則BG=CG=![]() cm
cm
∴AB=AG+BG=(![]() )cm
)cm
答:車架檔AB的長為![]() .
.


科目:初中數學 來源: 題型:
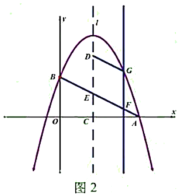
【題目】如圖1,在平面直角坐標系中,拋物線![]() 與
與![]() 軸的一個交點為點
軸的一個交點為點![]() ,與
,與![]() 軸的交點為點
軸的交點為點![]() ,拋物線的對稱軸
,拋物線的對稱軸![]() 與
與![]() 軸交于點
軸交于點![]() ,與線段
,與線段![]() 交于點
交于點![]() ,點
,點![]() 是對稱軸
是對稱軸![]() 上一動點.
上一動點.

(1)點![]() 的坐標是________,點
的坐標是________,點![]() 的坐標是________;
的坐標是________;
(2)是否存在點![]() ,使得
,使得![]() 和
和![]() 相似?若存在,請求出點
相似?若存在,請求出點![]() 的坐標,若不存在,請說明理由;
的坐標,若不存在,請說明理由;
(3)如圖2,拋物線的對稱軸![]() 向右平移與線段
向右平移與線段![]() 交于點
交于點![]() ,與拋物線交于點
,與拋物線交于點![]() ,當四邊形
,當四邊形![]() 是平行四邊形且周長最大時,求出點
是平行四邊形且周長最大時,求出點![]() 的橫坐標.
的橫坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,長、寬均為3,高為8的長方體容器,放置在水平桌面上,里面盛有水,水面高為6,繞底面一棱長進行旋轉傾斜后,水面恰好觸到容器口邊緣,圖2是此時的示意圖,則圖2中水面高度為( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α(0°<α≤90°),點F,G,P分別是DE,BC,CD的中點,連接PF,PG.
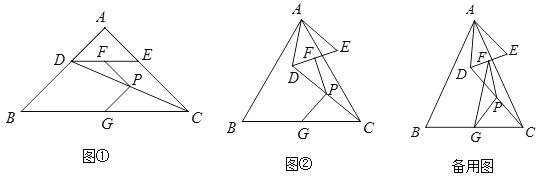
(1)如圖①,α=90°,點D在AB上,則∠FPG= °;
(2)如圖②,α=60°,點D不在AB上,判斷∠FPG的度數,并證明你的結論;
(3)連接FG,若AB=5,AD=2,固定△ABC,將△ADE繞點A旋轉,當PF的長最大時,FG的長為 (用含α的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是某班甲、乙、丙三位同學最近5次數學成績及其所在班級相應平均分的折線統計圖,則下列判斷錯誤的是( ).

A. 甲的數學成績高于班級平均分,且成績比較穩定
B. 乙的數學成績在班級平均分附近波動,且比丙好
C. 丙的數學成績低于班級平均分,但成績逐次提高
D. 就甲、乙、丙三個人而言,乙的數學成績最不穩
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某大樓的頂部樹有一塊廣告牌CD,小李在山坡的坡腳A處測得廣告牌底部D的仰角為60°.沿坡面AB向上走到B處測得廣告牌頂部C的仰角為45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的鉛直高度BH與水平寬度AH的比)
是指坡面的鉛直高度BH與水平寬度AH的比)

(1)求點B距水平面AE的高度BH;
(2)求廣告牌CD的高度.
(測角器的高度忽略不計,結果精確到0.1米.參考數據:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中數學 來源: 題型:
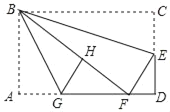
【題目】如圖,在矩形紙片ABCD中,AB=6,BC=10,點E在CD上,將△BCE沿BE折疊,點C恰落在邊AD上的點F處,點G在AF上,將△ABG沿BG折疊,點A恰落在線段BF上的點H處,有下列結論:①∠EBG=45°;②S△ABG=![]() S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正確的是_____.(把所有正確結論的序號都選上)
S△FGH;③△DEF∽△ABG;④AG+DF=FG.其中正確的是_____.(把所有正確結論的序號都選上)
查看答案和解析>>
科目:初中數學 來源: 題型:
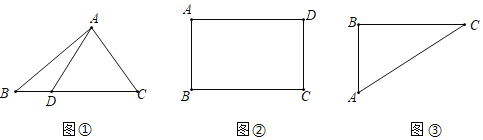
【題目】問題提出(1)如圖①,在△ABC中,BC=6,D為BC上一點,AD=4,則△ABC面積的最大值是 .
問題探究(2)如圖②,已知矩形ABCD的周長為12,求矩形ABCD面積的最大值.
問題解決(3)如圖③,△ABC是葛叔叔家的菜地示意圖,其中AB=30米,BC=40米,AC=50米,現在他想利用周邊地的情況,把原來的三角形地拓展成符合條件的面積盡可能大、周長盡可能長的四邊形地,用來建魚塘.已知葛叔叔欲建的魚塘是四邊形ABCD,且滿足∠ADC=60°.你認為葛叔叔的想法能否實現?若能,求出這個四邊形魚塘周長的最大值;若不能,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com