
【題目】近年來,為加強生態城市建設,邢臺市大力發展綠色交通,構建公共、綠色交通體系,2016年11月28日公共自行車陸續放置在車樁中,琪琪隨機調查了若干市民租用公共自行車的騎車時間:(單位:h),將獲得的數據分成五組,繪制了如下統計圖,請根據圖中信息,解答下列問題. 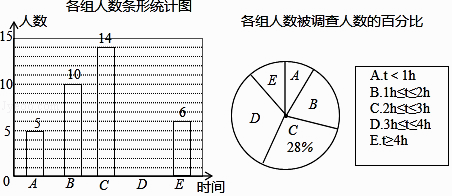
(1)這次被調查的總人數是多少?
(2)試求表示D組的扇形圓心角的度數,并補全條形統計圖;
(3)公共自行車系統投入使用后,按規定市民借車1小時內免費,1小時至2小時收費1元,2小時至3小時收費3元,3小時以上,在3元的基礎上,每小時加收3元(不足1小時均按1小時計算)請估算,在租用公共自行車的市民中,繳費超過3元的人數所占的百分比.
(4)A組5人中3女2男,從中隨機抽取2人,則恰好是一男一女的為事件A,用列表法或者樹狀圖法求出事件A的概率P.
【答案】
(1)解:被調查總人數為14÷28%=50人
(2)解:表示A組的扇形圓心角的度數為 ![]() ×360=108°;
×360=108°;
∵D組的人數為15人,
∴補全統計圖如圖所示:
(3)解:被調查的50人中,騎自行車的時間超過3元的人數為15+6=21人,
∴在租用公共自行車的市民中,繳費超過3元的人數所占的百分比= ![]() ×100%=42%;
×100%=42%;
(4)解:畫樹狀圖為:

共12種等可能的結果數,其中選中一男一女的結果數為12,
所以恰好選中一男一女的概率= ![]() =
= ![]()
【解析】(1)根據C組的人數和所占的百分比,即可求出這次被調查的總人數;(2)用360乘以D組所占的百分比,求出D組的扇形圓心角的度數,再用總人數減去A、B、D組的人數,求出C組的人數,從而補全統計圖;(3)求出租用公共自行車的市民中,繳費超過3元的人數即可得到所占的百分比;(4)畫樹狀圖展示所有12種等可能的結果數,再找出選中一男一女的結果數,然后根據概率公式求解.
【考點精析】認真審題,首先需要了解扇形統計圖(能清楚地表示出各部分在總體中所占的百分比.但是不能清楚地表示出每個項目的具體數目以及事物的變化情況),還要掌握條形統計圖(能清楚地表示出每個項目的具體數目,但是不能清楚地表示出各個部分在總體中所占的百分比以及事物的變化情況)的相關知識才是答題的關鍵.


科目:初中數學 來源: 題型:
【題目】“十一”國慶期間出租車司機小李某天下午的營運始終在長安街(自東向西或自西向東)上進行,如果規定向東為正,向西為負,他這天下午從天安門出發,行車里程(單位:千米)如下:
+15,﹣2,+5,﹣1,+10,﹣3,﹣2,+12,+4,﹣5,+6.
(1)小李將最后一名乘客送抵目的地時,小李距天安門有多遠?
(2)如果汽車耗油量為0.08升/千米,這天下午小李共耗油多少升?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線l上依次有三點A、B、C,且AB=8、BC=16,點P為射線AB上一動點,將線段AP進行翻折得到線段PA’(點A落在直線l上點A’處、線段AP上的所有點與線段PA’上的點對應)如圖1
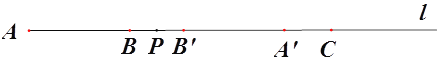
(1)若翻折后A’C=2,則翻折前線段AP= ;
(2)若點P在線段BC上運動,點M為線段A’C的中點,求線段PM的長度;
(3)若點P 在線段BC上運動,點N為B’P的中點,點M為線段A’C的中點,設AP=x,用x表示A’M+PN.

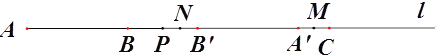
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從邊長為a的大正方形紙板中挖去一個邊長為b的小正方形后,將其裁成四個相同的等腰梯形(如圖1),然后拼成一個平行四邊形(如圖2)。那么通過計算兩個圖形的陰影部分的面積,可以驗證成立的公式是( )
A.a2-b2=(a-b)2 | B.(a+b)2="a+2ab+b" |
C.(a-b)2=a2-2ab+b2 | D.a2-b2=(a-b)(a+b) |

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在矩形ABCD中,已知AB=4,BC=3,矩形在直線l上繞其右下角的頂點B向右旋轉90°至圖①位置,再繞右下角的頂點繼續向右旋轉90°至圖②位置,…,以此類推,這樣連續旋轉2017次后,頂點A在整個旋轉過程中所經過的路程之和為 . 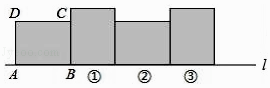
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,將一張正方形紙片剪成四個大小一樣的小正方形,然后將其中一個小正方形再按同樣的方法剪成四個小正方形,再將其中的一個小正方形剪成四個小正方形,如此循環進行下去。
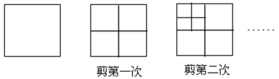
(1)完成下表:
剪的次數 | 1 | 2 | 3 | 4 | 5 | ... | n |
小正方形的個數 | 4 | 7 | 10 | ... |
|
(2)![]() .(用含n的代數式表示)
.(用含n的代數式表示)
(3)按上述方法,能否得到2018個小正方形?如果能,請求出n;如不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】根據題意解答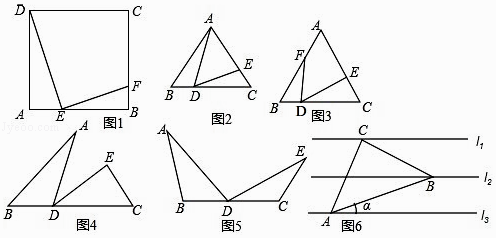
(1)如圖1,已知E是矩形ABCD的邊AB上一點,EF⊥DE交BC于點F,證明:△ADE∽△BFE.
(2)這個相似的基本圖形像字母K,可以稱為“K”型相似,但更因為圖形的結構特征是一條線上有3個垂直關系,也常被稱為“一線三垂直”,那普通的3個等角又會怎樣呢?
變式一如圖2,已知等邊三角形ABC,點D、E分別為BC,AC上的點,∠ADE=60°.
①圖中有相似三角形嗎?請說明理由.
②如圖3,若將∠ADE在△ABC的內部(∠ADE兩邊不與BC重合),繞點D逆時針旋轉一定的角度,還有相似三角形嗎?
(3)變式二如圖4,隱藏變式1圖形中的線段AE,在得到的新圖形中.
①如果∠B=∠C=∠ADE=50°,圖中有相似三角形嗎?請說明理由.
②如圖5,若∠B=∠C=∠ADE=∠a,∠a為任意角,還有相似三角形嗎?
(4)交式三已知,相鄰兩條平形直線間的距離相等,若等腰直角△ABC的三個頂點分別在這三條平行直線上,則cosa的值是(直接寫出結果).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是王老師在數學課堂上給同學們出的一道數學題,要求對以下實數進行分類填空:
-![]() ,0,
,0,![]() ,
,![]() ,18,
,18,![]() ,
,![]() ,-0.56,3.14159,
,-0.56,3.14159,![]() ,
,![]() ,
,![]() ,0.8080080008…,-
,0.8080080008…,-![]() .
.
(1)有理數集合:________________________________________________________________________;
(2)無理數集合:________________________________________________________________________;
(3)非負整數集合:________________________________________________________________________;
(4)分數集合:________________________________________________________________________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在菱形ABCD中,AB=6,∠DAB=60°,點E在BC邊上,且CE=2,AE與BD交于點F,連接CF,則下列結論不正確的是( ) 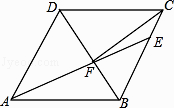
A.△ABF≌△CBF
B.△ADF∽△EBF
C.tan∠EAB= ![]()
D.S△EAB=6 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com