
【題目】如圖,小明同學用自制的直角三角形紙板DEF測量樹AB的高度,他調整自己的位置,設法使斜邊DF保持水平,并且邊DE與點B在同一直線上,已知紙板的兩條直角邊DE=40cm,EF=20cm,測得邊DF離地面的高度AC=1.5m,CD=8m,求樹AB的高度.

科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,A、B為x軸上兩點,C、D為y軸上的兩點,經過點A、C、B的拋物線的一部分c1與經過點A、D、B的拋物線的一部分c2組合成一條封閉曲線,我們把這條封閉曲線成為“蛋線”.已知點C的坐標為(0,﹣![]() ),點M是拋物線C2:y=mx2﹣2mx﹣3m(m<0)的頂點.
),點M是拋物線C2:y=mx2﹣2mx﹣3m(m<0)的頂點.
(1)求A、B兩點的坐標;
(2)“蛋線”在第四象限上是否存在一點P,使得△PBC的面積最大?若存在,求出△PBC面積的最大值;若不存在,請說明理由;
(3)當△BDM為直角三角形時,求m的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為推動陽光體育活動的廣泛開展,引導學生積極參加體育鍛煉,學校準備購買一批運動鞋供學生借用.現從各年級隨機抽取了部分學生的鞋號,繪制了如下的統計圖①和圖②,請根據圖中提供的信息,解答下列問題:

(1)本次接受隨機抽樣調查的學生人數為 人,圖①中的m的值為 ,圖①中“38號”所在的扇形的圓心角度數為 ;
(2)本次調查獲取的樣本數據的眾數是 ,中位數是 ;
(3)根據樣本數據,若學校計劃購買200雙運動鞋,建議購買36號運動鞋多少雙?
查看答案和解析>>
科目:初中數學 來源: 題型:
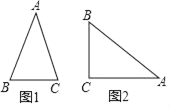
【題目】背景閱讀:我們在教材24.3已經知道了直角三角形中銳角的三角函數的概念,類似地,我們在等腰三角形中建立邊角之間的關系,即等腰三角形中底邊與腰的比叫做頂角的正對,記作:sad.如圖1,在△ABC中,AB=AC,頂角A的正對記作:sadA,這時sadA=![]() =
=![]() .
.
問題解決:
(1)若頂角A=60°,求sadA的值;
(2)若90°<∠A<180°,求∠A的正對sadA的取值范圍;
合作交流:
(3)如圖2,在Rt△ABC中,∠ACB=90°,若sinA=![]() ,試求以AC為腰的等腰三角形中,頂角A的正對sadA的值.
,試求以AC為腰的等腰三角形中,頂角A的正對sadA的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知O是直線AB上一點,∠BOE=∠FOD=90°,OB平分∠COD
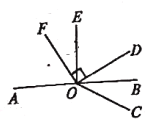
(1)圖中與∠DOE互余的角是______________________
(2)圖中是否有與∠DOE互補的角?如果有,直接寫出全部結果;如果沒有,說明理由。
(3)如果∠EOD︰∠EOF=3︰2,求∠AOC的度數
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩地相距300千米,一輛貨車和一輛轎車分別從甲地開往乙地![]() 轎車的平均速度大于貨車的平均速度
轎車的平均速度大于貨車的平均速度![]() ,如圖,線段OA、折線BCD分別表示兩車離甲地的距離
,如圖,線段OA、折線BCD分別表示兩車離甲地的距離![]() 單位:千米
單位:千米![]() 與時間
與時間![]() 單位:小時
單位:小時![]() 之間的函數關系.
之間的函數關系.
![]() 線段OA與折線BCD中,______表示貨車離甲地的距離y與時間x之間的函數關系.
線段OA與折線BCD中,______表示貨車離甲地的距離y與時間x之間的函數關系.
![]() 求線段CD的函數關系式;
求線段CD的函數關系式;
![]() 貨車出發多長時間兩車相遇?
貨車出發多長時間兩車相遇?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AD=10,AB=14,點E為DC上一個動點,若將△ADE沿AE折疊,當點D的對應點D′落在∠ABC的角平分線上時,則點D′到AB的距離為( )

A. 6 B. 6或8 C. 7或8 D. 6或7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】瑞士著名數學家歐拉發現:簡單多面體的頂點數V、面數F及棱數E之間滿足一種有趣的關系:V+F﹣E=2,這個關系式被稱為歐拉公式.比如:正二十面體(如右圖),是由20個等邊三角形所組成的正多面體,已知每個頂點處有5條棱,則可以通過歐拉公式算出正二十面體的頂點為_____個.那么一個多面體的每個面都是五邊形,每個頂點引出的棱都有3條,它是一個_____面體.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com