
【題目】在平面直角坐標系xOy中,直線l1:y=k1x+2![]() 與x軸、y軸分別交于點A、B兩點,OA=
與x軸、y軸分別交于點A、B兩點,OA=![]() OB,直線l2:y=k2x+b經過點C(1,﹣
OB,直線l2:y=k2x+b經過點C(1,﹣![]() ),與x軸、y軸和線段AB分別交于點E、F、D三點.
),與x軸、y軸和線段AB分別交于點E、F、D三點.
(1)求直線l1的解析式;
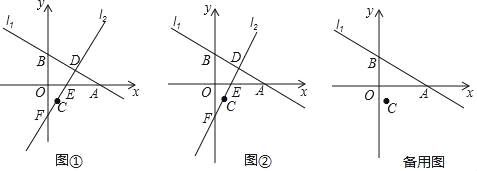
(2)如圖①:若EC=ED,求點D的坐標和△BFD的面積;
(3)如圖②:在坐標軸上是否存在點P,使△PCD是以CD為底邊的等腰直角三角形,若存在,請直接寫出點P的坐標;若不存在,請說明理由.
【答案】(1)![]() ;(2)D(3,
;(2)D(3,![]() ),面積為6
),面積為6![]() ;(3)存在,滿足條件的點P坐標為(0,4
;(3)存在,滿足條件的點P坐標為(0,4![]() ﹣6)或(2
﹣6)或(2![]() ,0),理由見解析
,0),理由見解析
【解析】
(1)求出點A的坐標,利用待定系數法即可解決問題;
(2)如圖1中,作CM⊥OA于M,DN⊥CA于N.由△CME≌△DNE(AAS),推出CM=DN由C(1,﹣![]() ),可得CM=DN=
),可得CM=DN=![]() ,再利用待定系數法即可解決問題;
,再利用待定系數法即可解決問題;
(3)分點P在y軸或x軸兩種情形分別求解即可解決問題;
解:(1)∵直線y=k1x+2![]() 與y軸B點,
與y軸B點,
∴B(0,2![]() ),
),
∴OB=2![]() ,
,
∵OA=![]() OB=6,
OB=6,
∴A(6,0),
把A(6,0)代入y=k1x+2![]() 得到,k1=﹣
得到,k1=﹣![]() ,
,
∴直線l1的解析式為y=﹣![]() x+2
x+2![]() .
.
(2)如圖1中,作CM⊥OA于M,DN⊥CA于N.
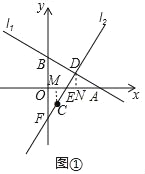
∵∠CME=∠DNE=90°,∠MEC=∠NED,EC=DE,
∴△CME≌△DNE(AAS),
∴CM=DN
∵C(1,﹣![]() ),
),
∴CM=DN=![]() ,
,
當y=![]() 時,
時,![]() =﹣
=﹣![]() x+2
x+2![]() ,
,
解得x=3,
∴D(3,![]() ),
),
把C(1,﹣![]() ),D(3,
),D(3,![]() )代入y=k2x+b,得到
)代入y=k2x+b,得到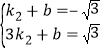 ,
,
解得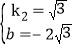 ,
,
∴直線CD的解析式為y=![]() x﹣2
x﹣2![]() ,
,
∴F(0,﹣2![]() ),
),
∴S△BFD=![]() ×4
×4![]() ×3=6
×3=6![]() .
.
(3)①如圖③﹣1中,當PC=PD,∠CPD=90°時,作DM⊥OB于M,CN⊥y軸于N.設P(0,m).
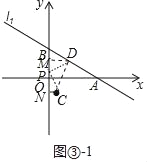
∵∠DMP=∠CNP=∠CPD=90°,
∴∠CPN+∠PCN=90°,∠CPN+∠DPM=90°,
∴∠PCN=∠DPM,
∵PD=PC,
∴△DMP≌△NPC(AAS),
∴CN=PM=1,PN=DM=m+![]() ,
,
∴D(m+![]() ,m+1),
,m+1),
把D點坐標代入y=﹣![]() x+2
x+2![]() ,得到:m+1=﹣
,得到:m+1=﹣![]() (m+
(m+![]() )+2
)+2![]() ,
,
解得m=4![]() ﹣6,
﹣6,
∴P(0,4![]() ﹣6).
﹣6).
②如圖③﹣2中,當PC=PC,∠CPD=90時,作DM⊥OA于M,CN⊥OA于N.設P(n,0).
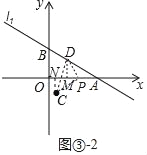
同法可證:△AMD≌△PNC,
∴PM=CN=![]() ,DM=PN=n﹣1,
,DM=PN=n﹣1,
∴D(n﹣![]() ,n﹣1),
,n﹣1),
把D點坐標代入y=﹣![]() x+2
x+2![]() ,得到:n﹣1=﹣
,得到:n﹣1=﹣![]() (n﹣
(n﹣![]() )+2
)+2![]() ,
,
解得n=2![]()
∴P(2![]() ,0).
,0).
綜上所述,滿足條件的點P坐標為(0,4![]() ﹣6)或(2
﹣6)或(2![]() ,0)
,0)


科目:初中數學 來源: 題型:
【題目】如圖,直角梯形AOCD的邊OC在x軸上,O為坐標原點,CD垂直于x軸,D(5,4),AD=2.若動點E、F同時從點O出發,E點沿折線OA→AD→DC運動,到達C點時停止;F點沿OC運動,到達C點時停止,它們運動的速度都是每秒1個單位長度.設E運動x秒時,△EOF的面積為y(平方單位),則y關于x的函數圖象大致為( )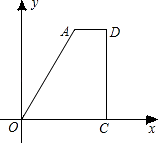
A.
B.
C.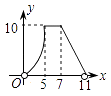
D.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果三個數a、b、c滿足其中一個數的兩倍等于另外兩個數的和,我們稱這三個數a、b、c是“等差數”若正比例函數y=2x的圖象上有三點A(![]() m﹣1,y1)、B(m,y2)、C(2m+1,y3),且這三點的縱坐標y1、y2、y3是“等差數”,則m=_____.
m﹣1,y1)、B(m,y2)、C(2m+1,y3),且這三點的縱坐標y1、y2、y3是“等差數”,則m=_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知![]() 四個點.
四個點.
(1)在圖中描出![]() ,
,![]() ,
,![]() ,
,![]() 四個點,順次連接
四個點,順次連接![]() 四點;
四點;
(2)直接寫出線段![]() 之間的位置關系_____________;
之間的位置關系_____________;
(3)求四邊形![]() 的面積
的面積
(4)將四邊形![]() 向右平移2個單位長度,向上平移4個單位長度得到四邊形
向右平移2個單位長度,向上平移4個單位長度得到四邊形![]() 寫出各頂點坐標
寫出各頂點坐標![]() ___________,
___________,![]() ____________,
____________,![]() ____________,
____________,![]() ____________.
____________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:我們把分一條線段為兩條相等線段的點稱為線段的中點.如圖1所示,則稱點M為線段AB的中點.
問題解決:
(1)如圖2所示,點A、B、C、D、E在數軸上的對應的數分別為﹣2、﹣1、0、1、2,則圖2中,線段AC的中點是點 ,點C是線段 和線段 的中點,線段AB的中點對應的數是 ,線段BE的中點對應的數是 ;
(2)如圖3,點E、F對應的數分別是e、f,則線段EF的中點對應的數為 (用含e、f的代數式表示).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一個長5m的梯子AB,斜靠在一豎直的墻AO上,這時AO的距離為4m,如果梯子的頂端A沿墻下滑1m至C點.
(1)求梯子底端B外移距離BD的長度;
(2)猜想CE與BE的大小關系,并證明你的結論.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算下列各題:
(1)(﹣x2+3y)(﹣2xy)
(2)[5xy2(x2﹣3xy)+(3x2y2)3]÷(5xy)2
(3)(﹣4x﹣3y2)(3y2﹣4x)
(4)(a+b)(a2﹣ab+b2)
(5)a(a﹣b)2﹣2b(a﹣b)(a+b)
(6)10002﹣998×1002(簡便運算).
(7)(3a2+![]() )(3a2﹣
)(3a2﹣![]() b)(9a4﹣
b)(9a4﹣![]() b2)
b2)
(8)(a2﹣ab+b2)(a2+ab+b2).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】聰聰是一位非常喜歡動腦筋的初一學生,特別是學了幾何后,更覺得數學奇妙,當聰聰學完![]() 圖形的初步知識
圖形的初步知識![]() 后對角平分線興趣更濃厚,下面請你和聰聰同學一起來探究奇妙的角平分線吧
后對角平分線興趣更濃厚,下面請你和聰聰同學一起來探究奇妙的角平分線吧![]() 已知
已知![]() ,射線OE,OF分別是
,射線OE,OF分別是![]() 和
和![]() 的角平分線.
的角平分線.
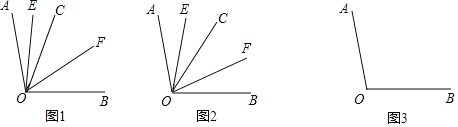
![]() 如圖1,若射線OC在
如圖1,若射線OC在![]() 的內部,且
的內部,且![]() ,求
,求![]() 的度數;
的度數;
![]() 如圖2,若射線OC在
如圖2,若射線OC在![]() 的內部繞點O旋轉,且
的內部繞點O旋轉,且![]() ,求
,求![]() 的度數;
的度數;
![]() 若射線OC在
若射線OC在![]() 的外部繞點O旋轉
的外部繞點O旋轉![]() 旋轉中
旋轉中![]() ,
,![]() 均指小于
均指小于![]() 的角
的角![]() ,其余條件不變,請借助圖3探究
,其余條件不變,請借助圖3探究![]() 的大小,請直接寫出
的大小,請直接寫出![]() 的度數
的度數![]() 不寫探究過程
不寫探究過程![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小李在某商場購買![]() 兩種商品若干次(每次
兩種商品若干次(每次![]() 商品都買) ,其中前兩次均按標價購買,第三次購買時,
商品都買) ,其中前兩次均按標價購買,第三次購買時,![]() 商品同時打折.三次購買
商品同時打折.三次購買![]() 商品的數量和費用如下表所示:
商品的數量和費用如下表所示:
購買A商品的數量/個 | 購買B商品的數量/個 | 購買總費用/元 | |
第一次 |
|
|
|
第二次 |
|
|
|
第三次 |
|
|
|
(1)求![]() 商品的標價各是多少元?
商品的標價各是多少元?
(2)若小李第三次購買時![]() 商品的折扣相同,則商場是打幾折出售這兩種商品的?
商品的折扣相同,則商場是打幾折出售這兩種商品的?
(3)在(2)的條件下,若小李第四次購買![]() 商品共花去了
商品共花去了![]() 元,則小李的購買方案可能有哪幾種?
元,則小李的購買方案可能有哪幾種?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com