
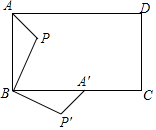
 如圖,P是矩形ABCD內一點,將△ABP繞點B順時針方向旋轉一定的角度后,AB能與CB重合,如圖.若PB=2,AB=3,BC=4,則P P′=2$\sqrt{2}$.
如圖,P是矩形ABCD內一點,將△ABP繞點B順時針方向旋轉一定的角度后,AB能與CB重合,如圖.若PB=2,AB=3,BC=4,則P P′=2$\sqrt{2}$. 分析 連接PP′,根據矩形的性質得到∠ABC=90°,再根據旋轉的性質得∠PBP′=∠ABC=90°,PB=P′B=2,則△PBP′為等腰直角三角形,然后根據等腰直角三角形的性質求解.
解答 解:連接PP′,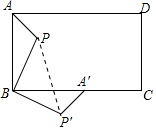
∵四邊形ABCD為矩形,
∴∠ABC=90°,
∵△ABP繞點B順時針方向旋轉能與△CBP′重合,
∴∠PBP′=∠ABC=90°,PB=P′B=2,
∴△PBP′為等腰直角三角形,
∴PP′=$\sqrt{2}$PB=2$\sqrt{2}$.
故答案為:2$\sqrt{2}$.
點評 本題考查了旋轉的性質,等腰直角三角形的判定與性質,正方形的性質,熟記各性質并判斷出△PBP′是等腰直角三角形是解題的關鍵.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 200(1+m%)2=148 | B. | 200(1-m%)2=148 | C. | 200(1-2m%)2=148 | D. | 200[1-(m%)2]=148 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com