8個人乘速度相同的兩輛小汽車同時趕往火車站,每輛車乘4人(不包括司機).其中一輛小氣車在距火車站10km的地方出現故障,此時距停止檢票的時間還有28分鐘.這時唯一可以利用的交通工具是另一輛小氣車,已知包括司機在內這輛車限乘5人,且這輛車的平均速度是60km/h.人步行的平均速度是5km/h.試設計一種方案,通過計算說明這8人能夠在停止檢票前趕到火車站.
解:當汽車出現故障時,乘這輛車的4人下車步行,另一輛車將自己車內的4人送到車站再回來接步行的4人再送至火車站;
設出現故障后乘這輛車的4人下車步行的距離為x,根據題意得:

=
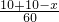
,解得x=

,
則步行的4人到達車站的用時為:

÷5+(10-

)÷60=
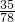
(小時)=26

(分鐘);
∵26

分鐘<28分鐘,
∴此方案可行.
此題還可有其他方案,只要滿足出現故障后先步行的4人到達車站總共的用時,不超28分鐘則方案可行.
分析:當汽車出現故障時,乘這輛車的4人下車步行,另一輛車將自己車內的4人送到車站再回來接步行的4人再送至火車站,此時可以設出現故障后乘這輛車的4人下車步行的距離為x,根據人走的時間和車返回時接的時間相同,可列出方程,得解后即可得出現故障后先步行的4人到達車站總共的用時,如果不超28分鐘則方案可行.此題還可有其他方案,只要滿足出現故障后先步行的4人到達車站總共的用時,如果不超28分鐘則方案可行.
點評:本題考查了一元一次方程的應用,解題關鍵是要讀懂題目的意思,根據題目給出的條件,設計合適的方案,根據等量關系列出方程,再求解判斷方案是否可行.

 =
=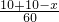 ,解得x=
,解得x= ,
, ÷5+(10-
÷5+(10- )÷60=
)÷60=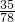 (小時)=26
(小時)=26 (分鐘);
(分鐘); 分鐘<28分鐘,
分鐘<28分鐘,

 閱讀快車系列答案
閱讀快車系列答案