【題目】有五張卡片，每張卡片上分別寫有1，2，3，4，5，洗勻后從中任取一張，放回后再抽一張，兩次抽到的數字和為_____的概率最大，抽到和大于8的概率為_____．
【答案】6 
【解析】
抽兩次牌總共有25種情況，分別求出數字和是2，3，4，5，6，7，8，9，10的情況個數，和大于8的個數，利用概率公式進行求解即可．
抽兩次牌總共有25種情況，
其中數字和是2的情況有1，1；
其中數字和是3的情況有1，2；2，1；
其中數字和是4的情況有1，3；2，2；3，1；
其中數字和是5的情況有1，4；2，3，3，2；4，1；
其中數字和是6的情況有1，5；2，4，3，3，4，2；5，1．
其中數字和是7的情況有2，5；3，4；4，3；5，2；
其中數字和是8的情況有3，5；5，3；4，4；
其中數字和是9的情況有4，5；5，4；
其中數字和是10的情況有5，5．
故兩次抽到的數字和為6的概率最大，抽到和大于8的概率為．
故答案為：6；．
名師金手指領銜課時系列答案科目：初中數學 來源： 題型：
【題目】2010年開始合肥市開展了“體育、藝術2+1”活動，我校根據實際情況，決定主要開設A：乒乓球，B：象棋，C：籃球，D：跳繩這四種運動項目．為了解學生喜歡哪一種項目，隨機抽取了部分學生進行調查，并將調查結果繪制成如圖甲、乙所示的條形統計圖和扇形統計圖．請你結合圖中的信息解答下列問題：
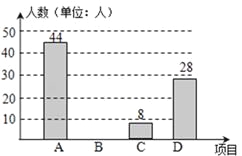
（1）樣本中喜歡B項目的人數百分比是 ，其所在扇形統計圖中的圓心角的度數是 ；
（2）把條形統計圖補充完整；
（3）已知我校有學生2400人，根據樣本估計全校喜歡乒乓球的人數是多少？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某市五月遭遇了持續強降雨，造成部分地區洪澇災害，某愛心組織緊急籌集了部分資金，計劃購買甲、乙兩種救災物品共4000件送往災區，已知每件甲種物品的價格比每件乙種物品的價格貴10元，用300元購買甲種物品的件數恰好與用240元購買乙種物品的件數相同.
（1）求甲、乙兩種救災物品每件的價格各是多少元？
（2）經調查，災區對乙種物品件數的需求量是甲種物品件數的3倍，若該愛心組織按照此需求的比例購買這4000件物品，需籌集資金多少元？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在矩形ABCD中，點E為邊AB上一點，且AE=
AB，EF⊥EC，連接BF．
（1）求證：△AEF∽△BCE；
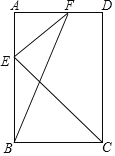
（2）若AB=3
，BC=3，求線段FB的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，直線y=﹣
x+c與x軸交于點A（3，0），與y軸交于點B，拋物線y=﹣
x2+bx+c經過點A，B．
（1）求點B的坐標和拋物線的解析式；
（2）M（m，0）為x軸上一動點，過點M且垂直于x軸的直線與直線AB及拋物線分別交于點P，N．
①點M在線段OA上運動，若以B，P，N為頂點的三角形與△APM相似，求點M的坐標；
②點M在x軸上自由運動，若三個點M，P，N中恰有一點是其它兩點所連線段的中點（三點重合除外），則稱M，P，N三點為“共諧點”．請直接寫出使得M，P，N三點成為“共諧點”的m的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】透明的口袋里裝有3個球，這3個球分別標有數字1、2、3，這些球除了數字外都相同。
（1）如果從袋中任意摸出一個球，那么摸到標有數字是2的球的概率是多少？（3分）
（2）小明和小東玩摸球游戲，游戲規則如下：先由小明隨機摸出一個球，記下球的數字后放回，攪勻后再由小東隨機摸出一個球，記下球的數字．誰摸出的球的數字大，誰獲勝．現請你利用樹狀圖或列表的方法分析游戲規則對雙方是否公平？并說明理由。（6分）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】現有甲、乙兩個體育用品商店出售乒乓球拍和乒乓球,球拍每塊價格為48元,乒乓球每個價格為2元，已知甲店制定的優惠方法是買--塊球拍送6個乒乓球,乙店按總價的
收費,某球隊需要購買球拍4塊,乒乓球
個(不少于24個)．
（1）試用含有的代數式表示甲、乙兩店購買球拍4塊,乒乓球個的費用．
（2）當需要購買240個乒乓球時,選擇哪家商店購買更優惠?請說明理由．
（3）當購買多少個乒乓球時,兩個商店的收費一樣多?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】目前“微信”、“支付寶”、“共享單車”和“網購”給我們帶來了很多便利，初二數學小組在校內對“你最認可的四大新生事物”進行了調查，隨機調查了
人（每名學生必選一種且只能從這四種中選擇一種）并將調查結果繪制成如下不完整的統計圖．
（1）根據圖中信息求出=___________，
=_____________；
（2）請你幫助他們將這兩個統計圖補全；
（3）根據抽樣調查的結果，請估算全校2000名學生種，大約有多少人最認可“微信”這一新生事物？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】下面是某同學對多項式(x2－2x)(x2－2x+2)+1進行因式分解的過程：
解：設x2－2x＝y
原式＝y (y+2)+1 （第一步）
＝y2+2y+1 （第二步）
＝(y+1)2 （第三步）
＝(x2－2x+1)2 （第四步）
請問：
（1）該同學因式分解的結果是否徹底？ （填“徹底”或“不徹底”），若不徹底，則該因式分解的最終結果為 ；
（2）請你模仿上述方法，對多項式(x2－4x+2)(x2－4x+6)+4進行因式分解．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com