
【題目】學校美術組要去商店購買鉛筆和橡皮,若購買60支鉛筆和30塊橡皮,則需按零售價購買,共支付30元;若購買90支鉛筆和60塊橡皮,則可按批發價購買,共支付40.5元.已知每支鉛筆的批發價比零售價低0.05元,每塊橡皮的批發價比零售價低0.10元.
(1)求每支鉛筆和每塊橡皮的批發價各是多少元?
(2)小亮同學用4元錢在這家商店按零售價買同樣的鉛筆和橡皮(兩樣都要買,4元錢恰好用完),共有哪幾種購買方案?
【答案】(1)每支鉛筆的批發價為0.25元,每塊橡皮的批發價為0.3元;(2)小亮共有三種購買方案
【解析】
(1)設每支鉛筆的批發價為x元,每塊橡皮的批發價為y元,根據“若購買60支鉛筆和30塊橡皮,則需按零售價購買,共支付30元;若購買90支鉛筆和60塊橡皮,則可按批發價購買,共支付40.5元”,即可得出關于x,y的二元一次方程組,解之即可得出結論;
(2)設可以購買m支鉛筆,n塊橡皮,根據總價=單價×數量,即可得出關于m,n的二元一次方程,再結合m,n均為正整數即可得出各購買方案.
(1)設每支鉛筆的批發價為x元,每塊橡皮的批發價為y元,
依題意,得:![]() ,
,
解得:![]() .
.
答:每支鉛筆的批發價為0.25元,每塊橡皮的批發價為0.3元.
(2)設可以購買m支鉛筆,n塊橡皮,
依題意,得:(0.25+0.05)m+(0.3+0.1)n=4,
∴n=10﹣![]() m.
m.
∵m,n均為正整數,
∴![]() ,
,![]() ,
,![]() ,
,
∴小亮共有三種購買方案,方案1:購買4支鉛筆,7塊橡皮;方案2:購買8支鉛筆,4塊橡皮;方案3:購買12支鉛筆,1塊橡皮.


科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,一次函數y=kx+b(k,b都是常數,且k≠0)的圖象經過點(1,0)和(0,2).
(1)當﹣2<x≤3時,求y的取值范圍;
(2)已知點P(m,n)在該函數的圖象上,且m﹣n=4,求點P的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,甲、乙、丙三艘輪船從港口O出發,當分別行駛到A,B,C處時,經測量得,甲船位于港口的北偏東43°45′方向,乙船位于港口的北偏東76°35′方向,丙船位于港口的北偏西43°45′方向.
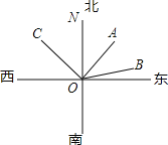
(1)求∠BOC的度數;
(2)求∠AOB的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD∥BC,且AD>BC,BC=6 cm,動點P,Q分別從A,C同時出發,P以1 cm/s的速度由A向D運動,Q以2cm/s的速度由C向B運動(Q運動到B時兩點同時停止運動),則________后四邊形ABQP為平行四邊形.
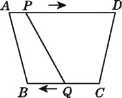
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系上有個點A(﹣1,0),點A第1次向上跳動1個單位至點A1(﹣1,1),緊接著第2次向右跳動2個單位至點A2(1,1),第3次向上跳動1個單位至點A3,第4次向左跳動3個單位至點A4,第5次又向上跳動1個單位至點A5,第6次向右跳動4個單位至點A6,……,依此規律跳動下去,點A第2019次跳動至點A2019的坐標是____.
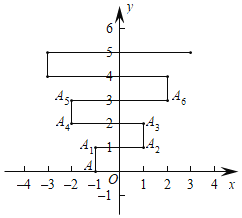
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】⑴ 閱讀理解
問題1:已知a、b、c、d為正數,![]() ,ac=bd,試說明a=d,b=c.
,ac=bd,試說明a=d,b=c.
我們通過構造幾何模型解決代數問題. 注意到條件![]() ,如果把a、b、c、d分別看作為兩個直角三角形的直角邊,那么可構造圖1所示的幾何模型.
,如果把a、b、c、d分別看作為兩個直角三角形的直角邊,那么可構造圖1所示的幾何模型.
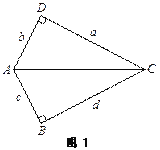
∵ac=bd,
∴AB·CD=BC·AD
∴![]()
請你按照以上思路繼續完成說明.
⑵ 深入探究
問題2:若a>0,b>0,試比較![]() 和
和![]() 的大小.
的大小.
為此我們構造圖2所示的幾何模型,其中AB為直徑, O為圓心,點C在半圓上,CD⊥AB 于D,AD=a,BD=b.
請你利用圖2所示的幾何模型解決提出的問題2.
⑶ 拓展運用
對于函數y=x+![]() ,求當x>0時,求y的取值范圍.
,求當x>0時,求y的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】老師在講“實數”時畫了一個圖(如圖),即“以數軸的單位長度為邊作一個正方形,然后以原點為圓心,正方形的對角線長為半徑畫弧交數軸于點A.

(1)A點表示的數是多少?在數軸上,A點與表示一1.42的點有什么位置關系;
(2)你認為老師作這樣的圖是為了說明什么?
(3)請類比上面的作法在數軸上畫出表示-![]() 的點B.(請保留作圖痕跡)
的點B.(請保留作圖痕跡)
查看答案和解析>>
科目:初中數學 來源: 題型:
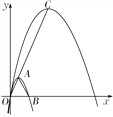
【題目】如圖,拋物線C1:y=-![]() x2+2
x2+2![]() x的頂點為A,與x軸的正半軸交于點B.
x的頂點為A,與x軸的正半軸交于點B.
(1)將拋物線C1上的點的橫坐標和縱坐標都擴大到原來的2倍,求變換后得到的拋物線的表達式;
(2)將拋物線C1上的點(x,y)變為(kx,ky)(|k|>1),變換后得到的拋物線記作C2,拋物線C2的頂點為C,求拋物線C2的表達式(用k表示);
(3)在(2)條件下,點P在拋物線C2上,滿足S△PAC=S△ABC,且∠ACP=90°.當k>1時,求k的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了測量豎直旗桿AB的高度,某綜合實踐小組在地面D處豎直放置標桿CD,并在地面上水平放置個平面鏡E,使得B,E,D在同一水平線上,如圖所示.該小組在標桿的F處通過平面鏡E恰好觀測到旗桿頂A(此時∠AEB=∠FED).在F處測得旗桿頂A的仰角為39.3°,平面鏡E的俯角為45°,FD=1.8米,問旗桿AB的高度約為多少米? (結果保留整數)(參考數據:tan39.3°≈0.82,tan84.3°≈10.02)

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com