
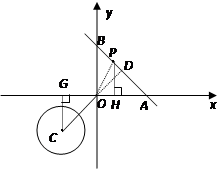
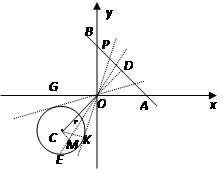
��D����ƽ��ֱ������(bi��o)ϵxOy�У���C�ĈA������(bi��o)�飨��2����2�����돽��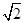 ������(sh��)y����x��2�ĈD���cx�S�����c(di��n)A���cy�S�����c(di��n)B���c(di��n)P��ֱ��AB��һ���c(di��n)��
������(sh��)y����x��2�ĈD���cx�S�����c(di��n)A���cy�S�����c(di��n)B���c(di��n)P��ֱ��AB��һ���c(di��n)��
��1������POA�ǵ��������Σ����c(di��n)P���c�c(di��n)A��B�غϣ�ֱ�ӌ����c(di��n)P������(bi��o)��
��2����(d��ng)ֱ��PO�c��C���Еr�����POA�ĶȔ�(sh��)��
��3����(d��ng)ֱ��PO�c��C�ཻ�r���O(sh��)���c(di��n)��E��F���c(di��n)M�龀��EF�����c(di��n)����PO��t��MO��s����s�ct֮�g�ĺ���(sh��)�P(gu��n)ϵʽ��������t��ȡֵ������
��1���t�c(di��n) ������(bi��o)�飨0��2������1��1������
������(bi��o)�飨0��2������1��1������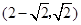 ��
��
��2�� ����
���� ��
�� ��3��
��3��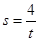 ����
����
����ԇ�}��������1�����L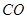 ��
�� ��
�� ���^�c(di��n)
���^�c(di��n) ��
��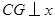 �S���c(di��n)
�S���c(di��n)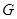 ��
��
��?y��n)�ֱ�� �ĺ���(sh��)�P(gu��n)ϵʽ��
�ĺ���(sh��)�P(gu��n)ϵʽ��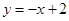 ��������
�������� ��
�� ��
��
����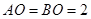 ��
��
����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/b0/c/16wip3.png" style="vertical-align:middle;" />������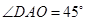 ��
��
��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/05/0/1xbi73.png" style="vertical-align:middle;" />������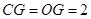 ��
��
����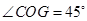 ��
��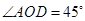 ��
��
���� ��
��
���� ����
���� ��
��
Ҫʹ ����������Σ�
�����������
�ٮ�(d��ng)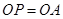 �r���˕r�c(di��n)
�r���˕r�c(di��n) �c�c(di��n)
�c�c(di��n)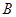 �غϣ������c(di��n)
�غϣ������c(di��n) ����(bi��o)�飨0��2����
����(bi��o)�飨0��2����
�ڮ�(d��ng) �r����
�r����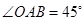 �������c(di��n)
�������c(di��n) ǡ����
ǡ���� �����c(di��n)�������c(di��n)
�����c(di��n)�������c(di��n) ����(bi��o)�飨1��1����
����(bi��o)�飨1��1����
�ۮ�(d��ng) �r���t
�r���t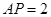 ���^�c(di��n)
���^�c(di��n) ��
��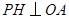 ��
��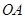 ���c(di��n)
���c(di��n)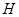 ����
���� ����
����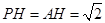 ������
������ �������c(di��n)
�������c(di��n) ������(bi��o)��
������(bi��o)��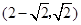 ��
��
���ԣ��� ����������Σ��t�c(di��n)
����������Σ��t�c(di��n) ������(bi��o)�飨0��2������1��1������
������(bi��o)�飨0��2������1��1������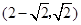 ��
��
��2����(d��ng)ֱ�� �c
�c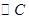 ���Еr���O(sh��)���c(di��n)��
���Еr���O(sh��)���c(di��n)�� ���B��
���B��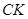 ���t
���t ��
��
���c(di��n) ������(bi��o)�飨
������(bi��o)�飨 ������
������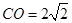 ��
��
����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/d3/4/1fc4s4.png" style="vertical-align:middle;" />�İ돽��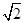 ������
������ ��
��
���� ����
����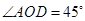 ������
������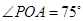 ��
��
ͬ������� �Ąeһ��ֵ��
�Ąeһ��ֵ�� ��
��
���� ����
���� ��
�� ��
��
��3����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/32/7/azw721.png" style="vertical-align:middle;" />��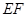 �����c(di��n)������
�����c(di��n)������ ��
��
����?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/7c/f/kwkal2.png" style="vertical-align:middle;" />��
����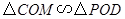 ��
��
���� ����
���� ��
��
��?y��n)?img src="http://thumb.zyjl.cn/pic5/tikupic/cf/c/oxx2a2.png" style="vertical-align:middle;" />������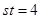 ��
��
��(d��ng) �^�A��
�^�A�� �r��
�r��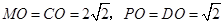 ����
����



| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
 ��D����ƽ��ֱ������(bi��o)�У���߅��OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬�c(di��n)P��x�S�ϵ�һ�����c(di��n)�������c(di��n)P���c�c(di��n)0���c(di��n)A�غϣ��B��CP��D�c(di��n)�Ǿ���AB��һ�c(di��n)���B��PD��
��D����ƽ��ֱ������(bi��o)�У���߅��OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬�c(di��n)P��x�S�ϵ�һ�����c(di��n)�������c(di��n)P���c�c(di��n)0���c(di��n)A�غϣ��B��CP��D�c(di��n)�Ǿ���AB��һ�c(di��n)���B��PD��| BD |
| AB |
| 5 |
| 8 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
 ��2012•�山�^(q��)һģ����D����ƽ��ֱ������(bi��o)xoy�У�������(bi��o)ԭ�c(di��n)O��A�ģ�3��돽���A���ĴˈA��(n��i)������߅�磩����������(sh��)�c(di��n)���M���v����(bi��o)��������(sh��)���������xȡһ���c(di��n)����M���v����(bi��o)֮�͞�0�ĸ�����
��2012•�山�^(q��)һģ����D����ƽ��ֱ������(bi��o)xoy�У�������(bi��o)ԭ�c(di��n)O��A�ģ�3��돽���A���ĴˈA��(n��i)������߅�磩����������(sh��)�c(di��n)���M���v����(bi��o)��������(sh��)���������xȡһ���c(di��n)����M���v����(bi��o)֮�͞�0�ĸ�����| 5 |
| 29 |
| 5 |
| 29 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
 ��D����ƽ��ֱ������(bi��o)�У���������ABCD���µ���x�S�ϣ���B�c(di��n)����(bi��o)�飨4��0����D�c(di��n)����(bi��o)�飨0��3�����tAC�L��
��D����ƽ��ֱ������(bi��o)�У���������ABCD���µ���x�S�ϣ���B�c(di��n)����(bi��o)�飨4��0����D�c(di��n)����(bi��o)�飨0��3�����tAC�L���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
 ��D����ƽ��ֱ������(bi��o)xOy�У���֪�c(di��n)A��-5��0����P�Ƿ���������(sh��)y=
��D����ƽ��ֱ������(bi��o)xOy�У���֪�c(di��n)A��-5��0����P�Ƿ���������(sh��)y=| k |
| x |
| k |
| x |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ�� �}�ͣ�
 ��COA=45�㣬���c(di��n)P���c(di��n)O���l(f��)��������OABC��߅���\(y��n)�ӣ�·����O��A��B��C�����_(d��)�c(di��n)C�rֹͣ����ֱ��CP��
��COA=45�㣬���c(di��n)P���c(di��n)O���l(f��)��������OABC��߅���\(y��n)�ӣ�·����O��A��B��C�����_(d��)�c(di��n)C�rֹͣ����ֱ��CP���鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com