
【題目】【發現證明】如圖1,點E,F分別在正方形ABCD的邊BC,CD上,∠EAF=45°,試判斷BE,EF,FD之間的數量關系.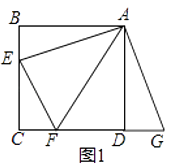
小聰把△ABE繞點A逆時針旋轉90°至△ADG,通過證明△AEF≌△AGF;從而發現并證明了EF=BE+FD.
(1)【類比引申】如圖2,點E、F分別在正方形ABCD的邊CB、CD的延長線上,∠EAF=45°,連接EF,請根據小聰的發現給你的啟示寫出EF、BE、DF之間的數量關系,并證明;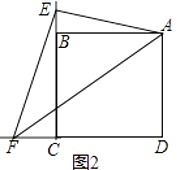
(2)【聯想拓展】如圖3,如圖,∠BAC=90°,AB=AC,點E、F在邊BC上,且∠EAF=45°,若BE=3,EF=5,求CF的長.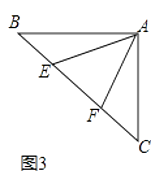
【答案】
(1)解:DF=EF+BE.
理由:如圖1所示,
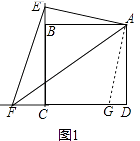
∵AB=AD,
∴把△ABE繞點A逆時針旋轉90°至△ADG,可使AB與AD重合,
∵∠ADC=∠ABE=90°,
∴點C、D、G在一條直線上,
∴EB=DG,AE=AG,∠EAB=∠GAD,
∵∠BAG+∠GAD=90°,
∴∠EAG=∠BAD=90°,
∵∠EAF=45°,
∴∠FAG=∠EAG﹣∠EAF=90°﹣45°=45°,
∴∠EAF=∠GAF,
在△EAF和△GAF中,
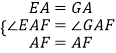 ,
,
∴△EAF≌△GAF,
∴EF=FG,
∵FD=FG+DG,
∴DF=EF+BE
(2)解:∵∠BAC=90°,AB=AC,
∴將△ABE繞點A順時針旋轉90°得△ACG,連接FG,如圖2,
∴AG=AE,CG=BE,∠ACG=∠B,∠EAG=90°,
∴∠FCG=∠ACB+∠ACG=∠ACB+∠B=90°,
∴FG2=FC2+CG2=BE2+FC2;
又∵∠EAF=45°,
而∠EAG=90°,
∴∠GAF=90°﹣45°,
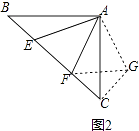
在△AGF與△AEF中,
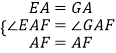 ,
,
∴△AEF≌△AGF,
∴EF=FG,
∴CF2=EF2﹣BE2=52﹣32=16,
∴CF=4.
【解析】(1)根據旋轉的性質和正方形的性質,得到EB=DG,AE=AG,∠EAB=∠GAD,由已知條件得到△EAF≌△GAF,根據全等三角形的對應邊相等,得到EF=FG,從而得到DF=EF+BE;(2)根據旋轉的性質和勾股定理,得到△AEF≌△AGF,根據全等三角形的對應邊相等,得到EF=FG,求出CF的長.
【考點精析】關于本題考查的正方形的性質和旋轉的性質,需要了解正方形四個角都是直角,四條邊都相等;正方形的兩條對角線相等,并且互相垂直平分,每條對角線平分一組對角;正方形的一條對角線把正方形分成兩個全等的等腰直角三角形;正方形的對角線與邊的夾角是45o;正方形的兩條對角線把這個正方形分成四個全等的等腰直角三角形;①旋轉后對應的線段長短不變,旋轉角度大小不變;②旋轉后對應的點到旋轉到旋轉中心的距離不變;③旋轉后物體或圖形不變,只是位置變了才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】閱讀材料:若![]() ,求m,n的值.
,求m,n的值.
解:![]() ,
,
![]() .
.
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
根據你的觀察,探究下面的問題:
(1)已知:![]() ,求
,求![]() 的值;
的值;
(2)已知:![]() 的三邊長a,b,c都是正整數,且滿足:
的三邊長a,b,c都是正整數,且滿足:![]() ,求
,求![]() 的最大邊c的值;
的最大邊c的值;
(3)已知:![]() ,
,![]() ,直接寫出a的值.
,直接寫出a的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD⊥BC,AE平分∠BAC,∠B=70°,∠C=30°.求:
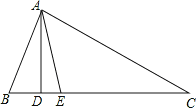
(1)∠BAE的度數;
(2)∠DAE的度數;
(3)探究:小明認為如果條件∠B=70°,∠C=30°改成∠B-∠C=40°,也能得出∠DAE的度數?若能,請你寫出求解過程;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知l1∥l2,MN分別和直線l1、l2交于點A、B,ME分別和直線l1、l2交于點C、D,點P在MN上(P點與A、B、M三點不重合).
(1)如果點P在A、B兩點之間運動時,∠α、∠β、∠γ之間有何數量關系請說明理由;
(2)如果點P在A、B兩點外側運動時,∠α、∠β、∠γ有何數量關系(只須寫出結論).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】老師所留的作業中有這樣一個分式的計算題:![]() ,甲、乙兩位同學完成的過程分別如下:
,甲、乙兩位同學完成的過程分別如下:

老師發現這兩位同學的解答都有錯誤.
(1)甲同學的解答從第 步開始出現錯誤,錯誤的原因是 ;
乙同學的解答從第 步開始出現錯誤,錯誤的原因是 ;
(2)請重新寫出完成此題的正確解答過程.
查看答案和解析>>
科目:初中數學 來源: 題型:
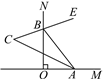
【題目】如圖,∠MON=90°,點A,B分別在射線OM,ON上運動,BE平分∠ABN,BE的反向延長線與∠BAO的平分線交于點C.
(1)當點A,B移動后,∠BAO=45°時,∠C=________;
(2)當點A,B移動后,∠BAO=60°時,∠C=________;
(3)由(1)(2)猜想∠C是否隨點A,B的移動而發生變化,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的袋子里裝有8個紅球,4個黃球,3個白球,他們除了顏色外都相同,兩人做游戲,游戲規則如下:一個人抓住袋子,一個人摸球,若摸出紅球,摸球者勝,否則拿袋子的人獲勝.
(1)如果你參加游戲,為了盡可能的獲勝,你是做摸球的人還是做拿袋子的人?為什么?
(2)你說這個游戲公平嗎?如果公平,說明理由:如果不公平,請給出修改建議,使它對雙方都是公平的.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在綜合與實踐課上,同學們以“一個含![]() 的直角三角尺和兩條平行線”為背景開展數學活動,如圖,已知兩直線
的直角三角尺和兩條平行線”為背景開展數學活動,如圖,已知兩直線![]() 且
且![]() 和直角三角形
和直角三角形![]() ,
,![]() ,
,![]() ,
,![]() .
.
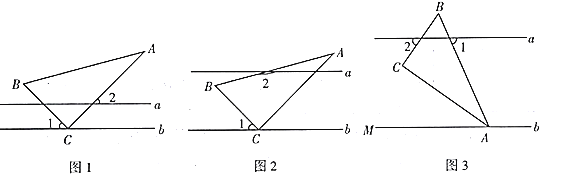
操作發現:
(1)在如圖1中,![]() ,求
,求![]() 的度數;
的度數;
(2)如圖2,創新小組的同學把直線![]() 向上平移,并把
向上平移,并把![]() 的位置改變,發現
的位置改變,發現![]() ,說明理由;
,說明理由;
實踐探究:
(3)縝密小組在創新小組發現結論的基礎上,將如圖中的圖形繼續變化得到如圖,![]() 平分
平分![]() ,此時發現
,此時發現![]() 與
與![]() 又存在新的數量關系,請直接寫出
又存在新的數量關系,請直接寫出![]() 與
與![]() 的數量關系.
的數量關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com