
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠BAC的平分線交BC于點O,OC=1,以點O為圓心OC為半徑作半圓.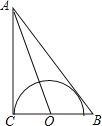
(1)求證:AB為⊙O的切線;
(2)如果tan∠CAO= ![]() ,求cosB的值.
,求cosB的值.
【答案】
(1)
解:如圖作OM⊥AB于M,
∵OA平分∠CAB,OC⊥AC,OM⊥AB,
∴OC=OM,
∴AB是⊙O的切線,
(2)
解:設BM=x,OB=y,則y2﹣x2=1 ①,
∵cosB= ![]() ,
,
∴ ![]() ,
,
∴x2+3x=y2+y ②,
由①②可以得到:y=3x﹣1,
∴(3x﹣1)2﹣x2=1,
∴x= ![]() ,y=
,y= ![]() ,
,
∴cosB= ![]() =
= ![]() .
.
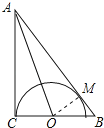
【解析】(1)如圖作OM⊥AB于M,根據角平分線性質定理,可以證明OM=OC,由此即可證明.(2)設BM=x,OB=y,列方程組即可解決問題.本題考查切線的判定、勾股定理、三角函數等知識,解題的關鍵是記住圓心到直線的距離等于半徑,這條直線就是圓的切線,學會設未知數列方程組解決問題,屬于中考常考題型.
【考點精析】解答此題的關鍵在于理解切線的判定定理的相關知識,掌握切線的判定方法:經過半徑外端并且垂直于這條半徑的直線是圓的切線,以及對銳角三角函數的定義的理解,了解銳角A的正弦、余弦、正切、余切都叫做∠A的銳角三角函數.


 互動課堂系列答案
互動課堂系列答案 激活思維智能訓練課時導學練系列答案
激活思維智能訓練課時導學練系列答案科目:初中數學 來源: 題型:
【題目】為了解七年級學生上學期參加社會實踐活動的情況,隨機抽查A市七年級部分學生參加社會實踐活動天數,并根據抽查結果制作了如下不完整的頻數分布表和條形統計圖.
A市七年級部分學生參加社會實踐活動天數的頻數分布表
天數 | 頻數 | 頻率 |
3 | 20 | 0.10 |
4 | 30 | 0.15 |
5 | 60 | 0.30 |
6 | a | 0.25 |
7 | 40 | 0.20 |
A市七年級部分學生參加社會實踐活動天數的條形統計圖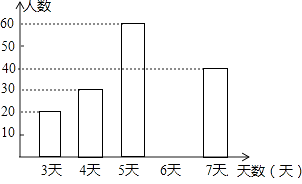
根據以上信息,解答下列問題;
(1)求出頻數分布表中a的值,并補全條形統計圖.
(2)A市有七年級學生20000人,請你估計該市七年級學生參加社會實踐活動不少于5天的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知在Rt△ABC中,∠ABC=90°,點D沿BC自B向C運動(點D與點B、C不重合),作BE⊥AD于E,CF⊥AD于F,則BE+CF的值( ) 
A.不變
B.增大
C.減小
D.先變大再變小
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某日,正在我國南海海域作業的一艘大型漁船突然發生險情,相關部門接到求救信號后,立即調遣一架直升飛機和一艘正在南海巡航的漁政船前往救援,當飛機到達海面3000m的高空C處時,測得A處漁政船的俯角為45°,測得B處發生險情漁船的俯角為30°,此時漁政船和漁船的距離AB是( ) 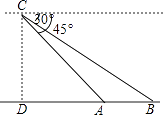
A.3000 ![]() m
m
B.3000( ![]() +1)m
+1)m
C.3000( ![]() -1)m
-1)m
D.1500 ![]() m
m
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形紙片ABCD中,AB=4,AD=12,將矩形紙片折疊,使點C落在AD邊上的點M處,折痕為PE,此時PD=3.
(1)求MP的值
(2)在AB邊上有一個動點F,且不與點A,B重合.當AF等于多少時,△MEF的周長最小?
(3)若點G,Q是AB邊上的兩個動點,且不與點A,B重合,GQ=2.當四邊形MEQG的周長最小時,求最小周長值.(計算結果保留根號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC內接于⊙O,弦AD⊥AB交BC于點E,過點B作⊙O的切線交DA的延長線于點F,且∠ABF=∠ABC. 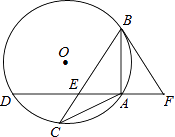
(1)求證:AB=AC;
(2)若AD=4,cos∠ABF= ![]() ,求DE的長.
,求DE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com