Question

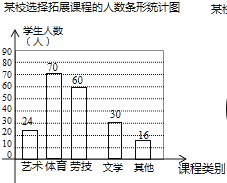
【題目】為深化義務教育課程改革，某校積極開展拓展性課程建設，計劃開設藝術、體育、勞技、文學等多個類別的拓展性課程，要求每一位學生都自主選擇一個類別的拓展性課程．為了了解學生選擇拓展性課程的情況，隨機抽取了部分學生進行調查，并將調查結果繪制成如下統計圖（部分信息未給出）：
根據統計圖中的信息，解答下列問題：
（1）求本次被調查的學生人數．
（2）將條形統計圖補充完整．
（3）若該校共有1600名學生，請估計全校選擇體育類的學生人數．

Answer 1

【答案】
（1）

解：60÷30%=200（人），

即本次被調查的學生有200人

（2）

解：選擇文學的學生有：200×15%=30（人），

選擇體育的學生有：200﹣24﹣60﹣30﹣16=70（人），

補全的條形統計圖如下圖所示，

（3）

解：1600× （人）．

即全校選擇體育類的學生有560人

【解析】（1）根據條形統計圖和扇形統計圖可知選擇勞技的學生60人，占總體的30%，從而可以求得調查學生人數；（2）根據文學的百分比和（1）中求得的學生調查數可以求得文學的有多少人，從而可以求得體育的多少人，進而可以將條形統計圖補充完整；（3）根據調查的選擇體育的學生所占的百分比可以估算出全校選擇體育類的學生人數．本題考查條形統計圖、用樣本估計總體、扇形統計圖，解題的關鍵是明確題意，找出所求問題需要的條件、利用數形結合的思想解答問題．