
【題目】我國古代數學的許多發現都曾位居世界前列,其中“楊輝三角”就是一例.下面我們依次對![]() 展開式的各項系數進一步研究發現,當
展開式的各項系數進一步研究發現,當![]() 取正整數時可以單獨列成表中的形式:
取正整數時可以單獨列成表中的形式:
例如,在三角形中第二行的三個數1,2,1,恰好對應![]() 展開式中的系數,
展開式中的系數,

(1)根據表中規律,寫出![]() 的展開式;
的展開式;
(2)多項式![]() 的展開式是一個幾次幾項式?并預測第三項的系數;
的展開式是一個幾次幾項式?并預測第三項的系數;
(3)請你猜想多項式![]() 取正整數)的展開式的各項系數之和(結果用含字母
取正整數)的展開式的各項系數之和(結果用含字母![]() 的代數式表示);
的代數式表示);
(4)利用表中規律計算:![]() (不用表中規律計算不給分).
(不用表中規律計算不給分).
【答案】(1)![]() ;(2)
;(2)![]() 次
次![]() 項式,第三項的系數為:
項式,第三項的系數為:![]() ;(3)
;(3)![]() ;(4)1.
;(4)1.
【解析】
(1)可以根據題意寫出答案,
(2)分別用![]() 、
、![]() 、
、![]() 去探究它們之間的關系,找出規律即可,
去探究它們之間的關系,找出規律即可,
(3)分別用![]() 、
、![]() 、
、![]() 先求出它們的系數和,找出規律即可,
先求出它們的系數和,找出規律即可,
(4)通過觀察可把正負號轉化為![]() 的偶次方和奇次方,然后把式子轉化為題中所給的形式即可得出答案.
的偶次方和奇次方,然后把式子轉化為題中所給的形式即可得出答案.
解:根據題意可得:
(1)觀察表中信息可寫出:![]() ,
,
(2)當![]() 時,多項式
時,多項式![]() 的展開式是一次二項式,此時第三項的系數為
的展開式是一次二項式,此時第三項的系數為![]() ,
,
當![]() 時,多項式
時,多項式![]() 的展開式是二次三項式,此時第三項的系數為
的展開式是二次三項式,此時第三項的系數為![]() ,
,
當![]() 時,多項式
時,多項式![]() 的展開式是三次四項式,此時第三項的系數為
的展開式是三次四項式,此時第三項的系數為![]() ,
,
![]()
![]() 多項式
多項式![]() 的展開式是一個
的展開式是一個![]() 次
次![]() 項式,
項式,
第三項的系數為:![]() ;
;
(3)當![]() 時,多項式
時,多項式![]() 的各項系數之和為:
的各項系數之和為:![]() ,
,
當![]() 時,多項式
時,多項式![]() 的各項系數之和為:
的各項系數之和為:![]() ,
,
當![]() 時,多項式
時,多項式![]() 的各項系數之和為:
的各項系數之和為:![]() ,
,
![]()
多項式![]() 展開式的各項系數之和為
展開式的各項系數之和為![]() :
:
(4)![]()
=![]()
=![]()
=1.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】如圖1,在△ABC中,AB=AC,D,E分別在AB,AC上,AD=AE,將△ADE繞點A逆時針任意旋轉.

(1)發現:如圖2,連結BD,CE,若∠BAC=60°,D點恰在線段BE上,則∠BEC= °;
(2)探究:如圖3,連結BD,CE,并交于點F,求證:∠BFC=∠BAC;
(3)拓展:如圖4,若∠BAC=90°,AB=5,AD=2,連結CD,BE,請直接寫出四邊形BCDE的最大面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一枚均勻的正方體骰子,六個面分別標有數字:1,2,3,4,5,6.如果用小剛拋擲正方體骰子朝上的數字x,小強拋擲正方體骰子朝上的數字y來確定點P(x,y),那么他們各拋擲一次所確定的點P落在已知直線y=﹣2x+7圖象上的概率是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在讀數月活動中學校準備購買一批課外讀物,為使課外讀物滿足同學們的需求,學校就“我最喜愛的課外讀物”從文學、藝術、科普和其他四個類別進行了抽樣調查(每位同學只選一類)。下圖是根據調查結果繪制的兩幅不完整的統計圖。

請你根據統計圖提供的信息,解答下列問題:
(1)本次調查中,一共調查了 名同學;
(2)條形統計圖中![]() ;
;
(3)扇形統計圖中,藝術類讀數所在扇形的圓心角是 度;
(4)學校計劃購買課外讀物8000冊,請根據樣本數據,估計學校購買其他類讀數多少冊?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2019年是中華人民共和國成立70周年,某校將開展“愛我中華,了解歷史”為主題的知識競賽,八年級某老師為了解所任教的甲,乙兩班學生相關知識的掌握情況,對兩個班的學生進行了中國歷史知識檢測,滿分為100分.現從兩個班分別隨機抽取了20名學生的檢測成績進行整理、描述和分析,下面給出了部分信息:(成績得分用x表示,共分為五組,A組:0≤x<80,B組:80≤x<85,C組:85≤x<90,D組:90≤x<95,E組:95≤x≤100)
甲班20名學生的成績為:
82,85,96,73,91,99,87,91,86,91
87, 94,89, 96,96,91,100,93,94, 99
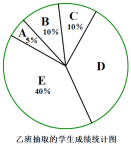
乙班20名學生的成績在D組中的數據是:91,92,92,92,92,93,94
甲,乙兩班抽取的學生成績數據統計表:
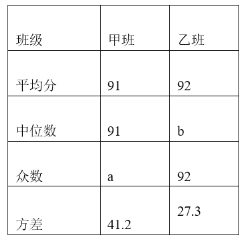
根據以上信息,解答下列問題:
(1)請直接寫出上述統計表中a,b的值:a= ,b= ;
(2)若甲,乙兩班總人數為120名,且都參加了此次知識檢測,若規定成績得分x≥95為優秀,請估計此次檢測成績優秀的學生人數是多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,己知,A(0, 4),B (t,0)分別在y軸,x軸上,連接AB,以AB為直角邊分別作等腰Rt△ABD和等腰Rt△ABC.直線BC交y軸于點E. 點G(-2,3)、H(-2,1)在第二象限內.

(1)當t =-3時,求點D的坐標.
(2)若點G、H位于直線AB的異側,確定t的取值范圍.
(3)①當t取何值時,△ABE與△ACE的面積相等.
②在①的條件下,在x軸上是否存在點P,使△PCB為等腰三角形?若存在,請直接寫出點P的坐標;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,直線![]() 與拋物線
與拋物線![]() 交于不同的兩點
交于不同的兩點![]() 、
、![]() (點
(點![]() 在點
在點![]() 的左側).
的左側).
(1)直接寫出![]() 的坐標 ; (用
的坐標 ; (用![]() 的代數式表示)
的代數式表示)
(2)設拋物線的頂點為![]() ,對稱軸
,對稱軸![]() 與直線
與直線![]() 的交點為
的交點為![]() ,連結
,連結![]() 、
、![]() ,若S△NDC=3×S△MDC,求拋物線的解析式;
,若S△NDC=3×S△MDC,求拋物線的解析式;
(3)如圖②,在(2)的條件下,設該拋物線與![]() 軸交于
軸交于![]() 、
、![]() 兩點,點
兩點,點![]() 為直線
為直線![]() 下方拋物線上一動點,連接
下方拋物線上一動點,連接![]() 、
、![]() ,設直線
,設直線![]() 交線段
交線段![]() 于點
于點![]() ,△MPQ的面積為
,△MPQ的面積為![]() ,△MAQ的面積為
,△MAQ的面積為![]() ,求
,求![]() 的最大值.
的最大值.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com