
【題目】銀泰百貨名創優品店購進600個鑰匙扣,進價為每個8元,第一周以每個12元的價格售出200個,第二周若按每個12元的價格銷售仍可售出200個,但商店為了適當增加銷量,決定降價銷售.據市場調查,單價每降低1元,可多售出50個,但售價不得低于進價,單價降低![]() 元銷售,銷售一周后,商店對剩余鑰匙扣清倉處理,以每個6元的價格全部售出.
元銷售,銷售一周后,商店對剩余鑰匙扣清倉處理,以每個6元的價格全部售出.
(1)如果這批鑰匙扣共獲利1050元,那么第二周每個鑰匙扣的銷售價格為多少元?
(2)這次降價活動,1050元是最高利潤嗎?若是,說明理由;若不是,求出最高利潤.
【答案】(1)9元;(2)1250元.
【解析】
(1)設獲利為w,根據每周的利潤等于每周的銷售量乘以(售價-進價),再將它們加起來,即可得w關于x的函數,然后讓其等于1050,解方程即可;
(2)將(1)中的利潤函數寫成頂點式,即可知最大值,從而可得結論.
(1)∵第二周每個旅游紀念品的銷售價格為(12-x)元,設獲利為w,由題意得:
w=200×(12-8)+(12-x-8)(200+50x)+(6-8)[(600-200)-(200+50x)]
=800+50(4-x)(4+x)-2(200-50x)
=800+800-50x2-400+100x
=-50x2+100x+1200
如果這批鑰匙扣共獲利1050元,則-50x2+100x+1200=1050
∴x2-2x-3=0
∴(x-3)(x+1)=0
∴x=3或x=-1(舍)
∴12-3=9(元)
∴第二周每個鑰匙扣的銷售價格為9元.
(2)∵w=-50x2+100x+1200
=-50(x-1)2+1250
∴當x=1時,w有最大值,最大值為1250元.
∴這次降價活動,1050元不是最高利潤,最高利潤是1250元.


 小天才課時作業系列答案
小天才課時作業系列答案 一課四練系列答案
一課四練系列答案 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,D為⊙O上一點,點C在直徑BA的延長線上,且∠CDA=∠CBD.
(1)求證:CD是⊙O的切線;
(2)過點B作⊙O的切線交CD的延長線于點E,BC=6, ![]() .求BE的長.
.求BE的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,平行四邊形ABCD,DE交BC于F,交AB的延長線于E,且∠EDB=∠C.
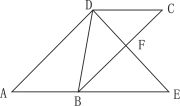
(1)求證:△ADE∽△DBE;
(2)若DE=9cm,AE=12cm,求DC的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】若自然數![]() 使得三個數的加法運算“
使得三個數的加法運算“![]() ”產生進位現象,則稱
”產生進位現象,則稱![]() 為“連加進位數”.例如:2不是“連加進位數”,因為
為“連加進位數”.例如:2不是“連加進位數”,因為![]() 不產生進位現象;4是“連加進位數”,因為
不產生進位現象;4是“連加進位數”,因為![]() 產生進位現象;51是“連加進位數”,因為
產生進位現象;51是“連加進位數”,因為![]() 產生進位現象.如果從0,1,2,…,99這100個自然數中任取一個數,取到“連加進位數”的個數有( )個
產生進位現象.如果從0,1,2,…,99這100個自然數中任取一個數,取到“連加進位數”的個數有( )個
A.88B.89C.90D.91
查看答案和解析>>
科目:初中數學 來源: 題型:
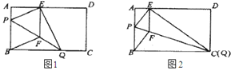
【題目】如圖![]() ,在矩形紙片
,在矩形紙片![]() 中,
中,![]() ,
,![]() ,折疊紙片使
,折疊紙片使![]() 點落在邊
點落在邊![]() 上的
上的![]() 處,折痕為
處,折痕為![]() .過點
.過點![]() 作
作![]() 交
交![]() 于
于![]() ,連接
,連接![]() .
.
(1)求證:四邊形![]() 為菱形;
為菱形;
(2)當點![]() 在
在![]() 邊上移動時,折痕的端點
邊上移動時,折痕的端點![]() ,
,![]() 也隨之移動.
也隨之移動.
①當點![]() 與點
與點![]() 重合時(如圖
重合時(如圖![]() ),求菱形
),求菱形![]() 的邊長;
的邊長;
②若限定![]() ,
,![]() 分別在邊
分別在邊![]() ,
,![]() 上移動,求出點
上移動,求出點![]() 在邊
在邊![]() 上移動的最大距離.
上移動的最大距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】九(1)班組織班級聯歡會,最后進入抽獎環節,每名同學都有一次抽獎機會,抽獎方案如下:將一副撲克牌中點數為“2”、“3”、“3”、“5”、“6”的五張牌背面朝上洗勻,先從中抽出1張牌,再從余下的4張牌中抽出1張牌,記錄兩張牌點數后放回,完成一次抽獎。記每次抽出兩張牌點數之差為x,按表格要求確定獎項.
獎項 | 一等獎 | 二等獎 | 三等獎 |
|
|
|
|
(1)用列表或畫樹狀圖的方法求出某同學抽一次獎獲一等獎的概率;
(2)抽一次獎獲一等獎的概率和不獲獎的概率相等嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線![]() 的頂點坐標為
的頂點坐標為![]() ,并且與
,并且與![]() 軸交于點
軸交于點![]() ,與
,與![]() 軸交于
軸交于![]() 、
、![]() 兩點.
兩點.
(![]() )求拋物線的表達式.
)求拋物線的表達式.
(![]() )如圖
)如圖![]() ,設拋物線的對稱軸與直線
,設拋物線的對稱軸與直線![]() 交于點
交于點![]() ,點
,點![]() 為直線
為直線![]() 上一動點,過點
上一動點,過點![]() 作
作![]() 軸的平行線
軸的平行線![]() ,與拋物線交于點
,與拋物線交于點![]() ,問是否存在點
,問是否存在點![]() ,使得以
,使得以![]() 、
、![]() 、
、![]() 為頂點的三角形與
為頂點的三角形與![]() 相似.若存在,求出點
相似.若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com