(2002•海淀區)已知:二次函數y=x2-kx+k+4的圖象與y軸交于點C,且與x軸的正半軸交于A、B兩點(點A在點B左側).若A、B兩點的橫坐標為整數,
(1)確定這個二次函數的解析式并求它的頂點坐標;
(2)若點D的坐標是(0,6),點P(t,0)是線段AB上的一個動點,它可與點A重合,但不與點B重合.設四邊形PBCD的面積為S,求S與t的函數關系式;
(3)若點P與點A重合,得到四邊形ABCD,以四邊形ABCD的一邊為邊,畫一個三角形,使它的面積等于四邊形ABCD的面積,并注明三角形高線的長.再利用“等底等高的三角形面積相等”的知識,畫一個三角形,使它的面積等于四邊形ABCD的面積(畫示意圖,不寫計算和證明過程).
【答案】
分析:(1)令y=0,不難得出方程的△>0;關鍵是方程的整數根,整除和奇偶性問題.根據(k-2+m)(k-2-m)=20得出k-2+m是k-2-m是同奇、同偶的兩數是解題的關鍵.
(由于k-2+m+k-2-m=2k-4,因此兩數的和為偶數,而偶數+偶數=偶數,奇數+奇數=偶數,奇數+偶數=奇數,因此兩數必須為同奇同偶)
(本題也可用韋達定理來求)
(2)由于四邊形PBCD不一定是規則的四邊形,因此可用三角形OBC的面積-三角形ODP的面積來求.
(3)本題答案不唯一,只要正確都行.
解答:解:(1)依題意可設A(a,0),B(b,0);
令y=0,則a、b是x
2-kx+k+4=0的兩根.
于是△=(-k)
2-4(k+4)=k
2-4k-16=(k-2)
2-20>0,且a+b=k;
∵a、b是不等的正整數,
∴k為正整數,且(k-2)
2-20是一個整數的平方.
設(k-2)
2-m
2=20,
即(k-2+m)(k-2-m)=20,
注意到k-2+m是k-2-m是同奇、同偶的兩數,且20是偶數.
∴
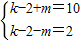
;
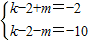
,

;
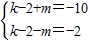
,
解得:

;
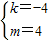
;
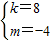
;

,
∴k=8,
∴這個二次函數的解析式為y=x
2-8x+12,其頂點坐標為(4,-4).
(2)∵y=x
2-8x+12,
∴此二次函數的圖形與y軸的交點C的坐標為(0,12),與y軸的交點A(2,0),B(6,0).
又S
四邊形PBCD=S
△COB-S
△DOP,
∴S=

×12×6-

×6t,
∴S=36-3t(2≤t<6);
(3)∵AB=4,又S=30,
∴可設所畫三角形為△MAB,AB邊上的高為h.
∴S
△MAB=

×4×h,
∴h=15.
點評:本題結合四邊形的性質考查二次函數的綜合應用,有關函數和幾何圖形的綜合題目,要利用幾何圖形的性質和二次函數的性質把數與形有機的結合在一起,利用題中所給出的面積和周長之間的數量關系求解.

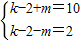 ;
;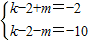 ,
, ;
;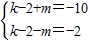 ,
, ;
;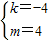 ;
;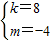 ;
; ,
, ×12×6-
×12×6- ×6t,
×6t, ×4×h,
×4×h,

 的解析式可確定為 .
的解析式可確定為 . ,求四邊形AECD的周長.
,求四邊形AECD的周長.