
【題目】在“綠滿重慶”行動中,江北區種植了大量的小葉榕和銀杏樹,根據林業專家的分析,樹葉在進行光合作用后產生的分泌物能在空氣中吸附懸浮顆粒,這樣就達到了滯塵凈化空氣的作用.
(1)若某小區今年要種植銀杏樹和小葉榕共450株,且銀杏樹的數量不超過小葉榕數量的2倍,求今年該小區小葉榕至少種植多少株?
(2)已知每一片銀杏樹葉一年平均滯塵量為![]() ,一株銀杏樹去年有3500片樹葉,冬季樹葉全部掉落后,今年新長出了樹葉,且這株銀杏今年的滯塵量是去年滯塵量的1.1倍還多
,一株銀杏樹去年有3500片樹葉,冬季樹葉全部掉落后,今年新長出了樹葉,且這株銀杏今年的滯塵量是去年滯塵量的1.1倍還多![]() .已知每片小葉榕樹葉的滯塵量比銀杏樹葉多
.已知每片小葉榕樹葉的滯塵量比銀杏樹葉多![]() ,一株小葉榕今年的樹葉總量比今年的這株銀杏要少
,一株小葉榕今年的樹葉總量比今年的這株銀杏要少![]() ,明年這株小葉榕樹葉將在今年的基礎上掉落
,明年這株小葉榕樹葉將在今年的基礎上掉落![]() ,但又會新長出1000片樹葉,若今明兩年這株小葉榕共滯塵量為
,但又會新長出1000片樹葉,若今明兩年這株小葉榕共滯塵量為![]() ,求
,求![]() 的值.
的值.
【答案】(1)該小區小葉榕至少種植150株;(2)該小區小葉榕至少種植150株,![]() 的值為35.
的值為35.
【解析】
(1)設今年該小區小葉榕種植x株,則銀杏樹種植(450-x)株,根據銀杏樹的數量不超過小葉榕數量的2倍,即可得出關于x的一元一次不等式,解之取其中的最小值即可得出結論;
(2)由這株銀杏今年的滯塵量是去年滯塵量的1.1倍還多1500mg可求出今年這株銀杏樹的樹葉數,根據滯塵總量=每片樹葉的滯塵量×樹葉數量結合今明兩年這株小葉榕共滯塵量為80000mg,即可得出關于a的一元二次方程,解之取其正值即可得出結論.
解:(1)設今年該小區小葉榕種植![]() 株,則銀杏樹種植
株,則銀杏樹種植![]() 株,
株,
由題意得:![]() ,
,
解得:![]()
∴該小區小葉榕至少種植150株.
(2)設今年這株銀杏有![]() 片樹葉,由題意得:
片樹葉,由題意得:
![]()
∴![]() ;
;
則有
![]()
令![]() ,整理化簡得
,整理化簡得
![]() .
.
解得:![]() ,
,![]() (舍),
(舍),
∴![]() ,
,
![]() .
.
答:該小區小葉榕至少種植150株,![]() 的值為35.
的值為35.


科目:初中數學 來源: 題型:
【題目】如圖,已知一次函數y=k1x+b的圖象分別與x軸、y軸的正半軸交于 A,B 兩點,且與反比例函數y= ![]() 交于 C,E 兩點,點 C 在第二象限,過點 C 作CD⊥x軸于點 D,AC=2
交于 C,E 兩點,點 C 在第二象限,過點 C 作CD⊥x軸于點 D,AC=2 ![]() ,OA=OB=1.
,OA=OB=1.
(1)△ADC 的面積;
(2)求反比例函數y= ![]() 與一次函數的y=k1x+b表達式.
與一次函數的y=k1x+b表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為深化義務教育課程改革,滿足學生的個性化學習需求,某校就“學生對知識拓展,體育特長、藝術特長和實踐活動四類選課意向”進行了抽樣調查(每人選報一類),繪制了如圖所示的兩幅統計圖(不完整),請根據圖中信息,解答下列問題:
(1)求扇形統計圖中m的值,并補全條形統計圖;
(2)在被調查的學生中,隨機抽一人,抽到選“體育特長類”或“藝術特長類”的學生的概率是多少?
(3)已知該校有800名學生,計劃開設“實踐活動類”課程每班安排20人,問學校開設多少個“實踐活動類”課程的班級比較合理?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知a,b,c分別是△ABC的三邊長,且滿足2a4+2b4+c4=2a2c2+2b2c2,則△ABC是( )
A. 等腰三角形 B. 等腰直角三角形
C. 直角三角形 D. 等腰三角形或直角三角形
【答案】B
【解析】解析:∵2a4+2b4+c4=2a2c2+2b2c2,∴4a4-4a2c2+c4+4b4-4b2c2+c4=0,
∴(2a2-c2)2+(2b2-c2)2=0,∴2a2-c2=0,2b2-c2=0,
∴c=2a,c=2b,
∴a=b,且a2+b2=c2,
∴△ABC為等腰直角三角形.
故選B.
【題型】單選題
【結束】
11
【題目】將圖1中陰影部分的小長方形變換到圖2的位置,你能根據兩個圖形的面積關系得到的數學公式是_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,平行四邊形![]() 的邊
的邊![]() 在
在![]() 軸上,點
軸上,點![]() ,線段
,線段![]() ,線段
,線段![]() ,且
,且![]() ,
,![]() 與
與![]() 的交點記為
的交點記為![]() ,連接
,連接![]() .
.
(1)求![]() 的面積.
的面積.
(2)如圖2,在線段![]() 上有兩個動點
上有兩個動點![]() 、
、![]() (
(![]() 在
在![]() 點上方),且
點上方),且![]() ,點
,點![]() 為
為![]() 中點,點
中點,點![]() 為線段
為線段![]() 上一動點,當
上一動點,當![]() 的值最小時,求出此時
的值最小時,求出此時![]() 點的坐標;
點的坐標;
(3)在(2)的條件下,在![]() 軸上找一點
軸上找一點![]() ,
,![]() 軸上找一點
軸上找一點![]() ,使得
,使得![]() 取得最小值,請求出
取得最小值,請求出![]() 的最小值.
的最小值.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知△ABC中,AC=BC,點D、E、F分別是線段AC、BC、AD的中點,BF、ED的延長線交于點G,連接GC.
(1)求證:AB=GD;
(2)當CG=EG時,且AB=2,求CE.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在ABCD中,∠ABD的平分線BE交AD于點E,∠CDB的平分線DF交BC于點F,連接BD.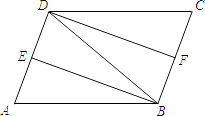
(1)求證:△ABE≌△CDF;
(2)若AB=DB,求證:四邊形DFBE是矩形.
查看答案和解析>>
科目:初中數學 來源: 題型:
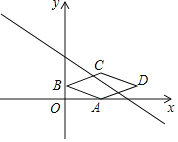
【題目】如圖,在平面直角坐標系xOy中,菱形ABCD的頂點A的坐標為(2,0),點B的坐標為(0,1),對角線BD與x軸平行,若直線y=kx+5+2k(k≠0)與菱形ABCD有交點,則k的取值范圍是( )
A.![]() B.
B.![]()
C.![]() D.﹣2≤k≤2且k≠0
D.﹣2≤k≤2且k≠0
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com