
【題目】已知y關于x的二次函數:y=![]() (m﹣n)x2+nx+t﹣n.
(m﹣n)x2+nx+t﹣n.
(1)當m=t=0時,判斷該函數圖象和x軸的交點個數;
(2)若n=t=3m,當x為何值時,函數有最值;
(3)是否存在實數m和t,使該函數圖象和x軸有交點,且n的最大值和最小值分別為8和4?若存在,求m和t值;若不存在,請說明理由.
【答案】(1)見解析(2)x=![]() 函數有最大值為
函數有最大值為![]() (3) 不存在實數m和t,使該函數圖象和x軸有交點
(3) 不存在實數m和t,使該函數圖象和x軸有交點
【解析】試題分析:(1)利用判別式求交點個數.(2)化簡二次函數,配方,求最值.(3)配方求最值,最值用n,m,t表示,假設且n的最大值和最小值分別為8和4,代入求m,t,無解.
試題解析:
(1)當m=t=0時,y=﹣![]() nx2+nx﹣n,
nx2+nx﹣n,
△=n2﹣4×(﹣![]() )n×(﹣n)=﹣n2,
)n×(﹣n)=﹣n2,
當n=0時,△=0,該函數圖象與x軸有1個交點;
當n≠0時,△<0,該函數圖象與x軸沒有交點;
(2)若n=t=3m,拋物線的解析式為:y=![]() (m﹣3m)x2+3mx=﹣mx2+3mx=﹣m(x﹣
(m﹣3m)x2+3mx=﹣mx2+3mx=﹣m(x﹣![]() )2+
)2+![]() ,
,
當﹣m>0,即m<0時,
所以當x=![]() 時,函數有最小值為
時,函數有最小值為![]() ,
,
當﹣m<0,即m>0時,
所以當x=![]() 時,函數有最大值為
時,函數有最大值為![]() ;
;
(3)y=![]() (m﹣n)x2+nx+t﹣n,
(m﹣n)x2+nx+t﹣n,
△=n2﹣4×![]() (m﹣n)(t﹣n)=﹣n2+2(m+t)n﹣2mt,
(m﹣n)(t﹣n)=﹣n2+2(m+t)n﹣2mt,
設w=﹣n2+2(m+t)n﹣2mt,
∵該函數圖象和x軸有交點,
∴w≥0,
∵n的最大值和最小值分別為8和4,
∴新二次函數w與n軸有兩個交點為(4,0)和(8,0),
則w=﹣(n﹣4)(n﹣8)=﹣n2+12n﹣32,
∴![]() ,
,
![]() ,
,
此方程組無實數解,
∴不存在實數m和t,使該函數圖象和x軸有交點.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】學校初一年級參加社會實踐課,報名第一門課的有x人,第二門課的人數比第一門課的![]() 少20人,現在需要從報名第二門課的人中調出10人學習第一門課,那么用含x的式子解答下題.
少20人,現在需要從報名第二門課的人中調出10人學習第一門課,那么用含x的式子解答下題.
(1)報兩門課的共有多少人?
(2)調動后,報名第一門課比報名第二門課多多少人?計算出代數式后,請選擇一個你覺得合適的x值代入,并求出具體人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
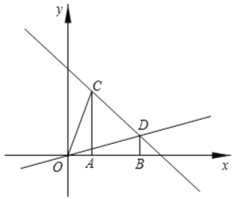
【題目】在平面直角坐標系中,過點C(1,3)、D(3,1)分別作x軸的垂線,垂足分別為A、B.
(1)求直線CD和直線OD的解析式;
(2)點M為直線OD上的一個動點,過M作x軸的垂線交直線CD于點N,是否存在這樣的點M,使得以A、C、M、N為頂點的四邊形為平行四邊形?若存在,求此時點M的橫坐標;若不存在,請說明理由;
(3)若△AOC沿CD方向平移(點C在線段CD上,且不與點D重合),在平移的過程中,設平移距離為![]() t,△AOC與△OBD重疊部分的面積記為s,試求s與t的函數關系式.
t,△AOC與△OBD重疊部分的面積記為s,試求s與t的函數關系式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 朗讀者
朗讀者![]() 自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級
自開播以來,以其厚重的文化底蘊和感人的人文情懷,感動了數以億計的觀眾,岳池縣某中學開展“朗讀”比賽活動,九年級![]() 、
、![]() 班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績
班根據初賽成績,各選出5名選手參加復賽,兩個班各選出的5名選手的復賽成績![]() 滿分為100分
滿分為100分![]() 如圖所示.
如圖所示.
平均數 | 中位數 | 眾數 | |
九 | 85 | 85 | |
九 | 80 |
![]() 根據圖示填寫表格;
根據圖示填寫表格;
![]() 結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
結合兩班復賽成績的平均數和中位數,分析哪個班級的復賽成績較好;
![]() 如果規定成績較穩定班級勝出,你認為哪個班級能勝出?說明理由.
如果規定成績較穩定班級勝出,你認為哪個班級能勝出?說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】從2開始,連續的偶數相加,它們和的情況如下表:
加數的個數n | S |
1 | 2=1×2 |
2 | 2+4=6=2×3 |
3 | 2+4+6=12=3×4 |
4 | 2+4+6+8=20=4×5 |
5 | 2+4+6+8+10=30=5×6 |
(1)若n=8時,則S的值為_____________.
(2)根據表中的規律猜想:用n的式子表示S的公式為:S=2+4+6+8+…+2n=__________________.
(3)根據上題的規律計算2+4+6+8+10+…+98+100![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店購進甲、乙兩種商品,已知每件甲種商品的價格比每件乙種商品的價格貴10元,用350元購買甲種商品的件數恰好與用300元購買乙種商品的件數相同.
(1)求甲、乙兩種商品每件的價格各是多少元?
(2)計劃購買這兩種商品共50件,且投入的經費不超過3200元,那么,最多可購買多少件甲種商品?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(閱讀理解題)在解分式方程![]() 時,小明的解法如下:
時,小明的解法如下:
解:方程兩邊都乘以x﹣3,得2﹣x=﹣1﹣2①.移項得﹣x=﹣1﹣2﹣2②.解得x③.
(1)你認為小明在哪一步出現了錯誤? (只寫序號),錯誤的原因是 .
(2)小明的解題步驟完善嗎?如果不完善,說明他還缺少哪一步?答: .
(3)請你解這個方程.
查看答案和解析>>
科目:初中數學 來源: 題型:
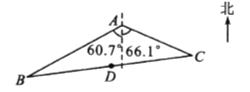
【題目】如圖,濕地景區岸邊有三個觀景臺![]() 、
、![]() 、
、![]() .已知
.已知![]() m,
m, ![]() m,點
m,點![]() 位于點
位于點![]() 的南偏西60. 7°方向,點
的南偏西60. 7°方向,點![]() 位于點
位于點![]() 的南偏東66. 1°方向.
的南偏東66. 1°方向.
(1)求![]() 的面積;
的面積;
(2)景區規劃在線段![]() 的中點
的中點![]() 處修建一個湖心亭,并修建觀景棧道
處修建一個湖心亭,并修建觀景棧道![]() .試求
.試求![]() 、
、![]() 間的距離.(結果精確到0. 1 m,參考數據:
間的距離.(結果精確到0. 1 m,參考數據: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在梯形ABCD中,AB∥CD,∠D=90°,AD=CD=2,點E在邊AD上(不與點A、D重合),∠CEB=45°,EB與對角線AC相交于點F,設DE=x.
(1)用含x的代數式表示線段CF的長;
(2)如果把△CAE的周長記作C△CAE,△BAF的周長記作C△BAF,設![]() =y,求y關于x的函數關系式,并寫出它的定義域;
=y,求y關于x的函數關系式,并寫出它的定義域;
(3)當∠ABE的正切值是![]() 時,求AB的長.
時,求AB的長.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com