
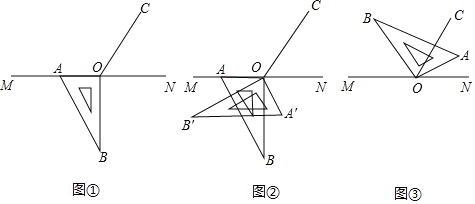
【題目】如圖①,點O為直線MN上一點,過點O作直線OC,使∠NOC=60°.將一把直角三角尺的直角頂點放在點O處,一邊OA在射線OM上,另一邊OB在直線AB的下方,其中∠OBA=30°
(1)將圖②中的三角尺沿直線OC翻折至△A′B′O,求∠A′ON的度數;
(2)將圖①中的三角尺繞點O按每秒10°的速度沿順時針方向旋轉,旋轉角為α(0<α<360°),在旋轉的過程中,在第幾秒時,直線OA恰好平分銳角∠NOC;
(3)將圖①中的三角尺繞點O順時針旋轉,當點A點B均在直線MN上方時(如圖③所示),請探究∠MOB與∠AOC之間的數量關系,請直接寫出結論,不必寫出理由.
【答案】(1)∠A′ON=60°;(2)第15或秒時,直線OA恰好平分銳角∠NOC;(3)①當OB,OA在OC的兩旁時,∠MOB-∠AOC=30°,②當OB,OA在OC的同側時,∠MOB+∠AOC=120°-90°=30°.
【解析】
(1)如圖②中,延長CO到C′.利用翻折不變性求出∠A′O′C′即可解決問題;
(2)設t秒時,直線OA恰好平分銳角∠NOC.構建方程即可解決問題;
(3)分兩種情形分別求解即可解決問題;
(1)如圖②中,延長CO到C′.
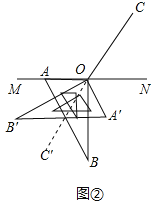
∵三角尺沿直線OC翻折至△A′B′O,
∴∠A′OC′=∠AOC′=∠CON=60°,
∴∠A′ON=180°-60°-60°=60°.
(2)設t秒時,直線OA恰好平分銳角∠NOC.
由題意10t=150或10t=330,
解得t=15或33s,
答:第15或秒時,直線OA恰好平分銳角∠NOC;
(3)①當OB,OA在OC的兩旁時,∵∠AOB=90°,
∴120°-∠MOB+∠AOC=90°,
∴∠MOB-∠AOC=30°.
②當OB,OA在OC的同側時,∠MOB+∠AOC=120°-90°=30°.


 浙江之星學業水平測試系列答案
浙江之星學業水平測試系列答案 高效智能課時作業系列答案
高效智能課時作業系列答案科目:初中數學 來源: 題型:
【題目】某校為了了解初中各年級學生每天的平均睡眠時間(單位:h,精確到1 h),抽樣調查了部分學生,并用得到的數據繪制了下面兩幅不完整的統計圖.
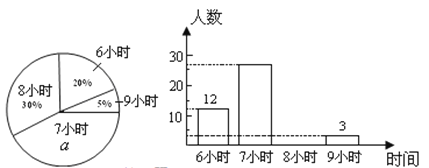
請你根據圖中提供的信息,回答下列問題:
(1)求出扇形統計圖中百分數![]() 的值為_______,所抽查的學生人數為______;
的值為_______,所抽查的學生人數為______;
(2)求出平均睡眠時間為8小時的人數,并補全條形圖;
(3)求出這部分學生的平均睡眠時間的平均數;
(4)如果該校共有學生1200名,請你估計睡眠不足(少于8小時)的學生數.
查看答案和解析>>
科目:初中數學 來源: 題型:
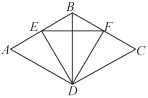
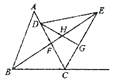
【題目】如圖,把等邊三角形ABD和等邊三角形BCD拼合在一起,點E在AB邊上移動,且滿足AE=BF,試說明不論點E怎樣移動,△EDF總是等邊三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于![]() 的方程組
的方程組![]() ,以下結論:
,以下結論:
①![]() 時,方程組的解也是方程
時,方程組的解也是方程![]() 的解;
的解;
②論![]() 取什么實數,
取什么實數,![]() 的值始終不變;
的值始終不變;
③若![]() ,則
,則![]() 的最小值為
的最小值為![]() ;
;
請判斷以上結論是否正確,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,某超市從底樓到二樓有一自動扶梯,圖2是側面示意圖.已知自動扶梯AB的坡度為1:2.4,AB的長度是13米,MN是二樓樓頂,MN∥PQ,C是MN上處在自動扶梯頂端B點正上方的一點,BC⊥MN,在自動扶梯底端A處測得C點的仰角為42°,求二樓的層高BC(精確到0.1米).
(參考數據:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)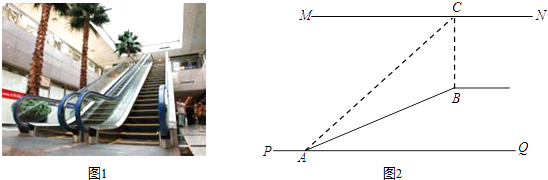
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在![]() 中,
中,![]() ,
,![]() 為
為![]() 邊
邊![]() 上一點,
上一點,![]() ,
,![]() 平分
平分![]() 的外角,且
的外角,且![]() .連接
.連接![]() 交
交![]() 于
于![]() 為邊
為邊![]() 上一點,滿足
上一點,滿足![]() ,連接
,連接![]() 交
交![]() 于
于![]() .以下結論:①
.以下結論:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 平分
平分![]() ,則
,則![]() 平分
平分![]() 正確的是_____________.
正確的是_____________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知一次函數y=(k﹣2)x﹣3k2+12.
(1)k為何值時,圖象經過原點;
(2)k為何值時,圖象與直線y=﹣2x+9的交點在y軸上;
(3)k為何值時,圖象平行于y=﹣2x的圖象;
(4)k為何值時,y隨x增大而減小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在等腰△ABC中,∠ACB=90°,且AC=1.過點C作直線l∥AB,P為直線l上一點,且AP=AB.則點P到BC所在直線的距離是( )
A.1
B.1或 ![]()
C.1或 ![]()
D.![]() 或
或 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com