
【題目】在平面直角坐標系中,借助直角三角板可以找到一元二次方程的實數根,比如對于方程 ![]() ,操作步驟是:
,操作步驟是:
第一步:根據方程系數特征,確定一對固定點A(0,1),B(5,2);
第二步:在坐標平面中移動一個直角三角板,使一條直角邊恒過點A,另一條直角邊恒過點B;
第三步:在移動過程中,當三角板的直角頂點落在x軸上點C處時,點C 的橫坐標m即為該方程的一個實數根(如圖1)
第四步:調整三角板直角頂點的位置,當它落在x軸上另一點D處時,點D 的橫坐標為n即為該方程的另一個實數根。
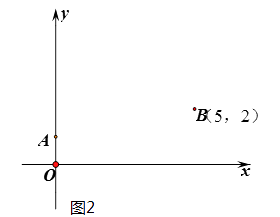
(1)在圖2 中,按照“第四步“的操作方法作出點D(請保留作出點D時直角三角板兩條直角邊的痕跡)
(2)結合圖1,請證明“第三步”操作得到的m就是方程 ![]() 的一個實數根;
的一個實數根;
(3)上述操作的關鍵是確定兩個固定點的位置,若要以此方法找到一元二次方程 ![]() 的實數根,請你直接寫出一對固定點的坐標;
的實數根,請你直接寫出一對固定點的坐標;
(4)實際上,(3)中的固定點有無數對,一般地,當 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 與a,b,c之間滿足怎樣的關系時,點P(
與a,b,c之間滿足怎樣的關系時,點P( ![]() ,
, ![]() ),Q(
),Q( ![]() ,
, ![]() )就是符合要求的一對固定點?
)就是符合要求的一對固定點?
【答案】
(1)
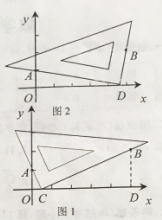
解:如圖2所示:
(2)
證明:在圖1中,過點B作BD⊥x軸,交x軸于點D.
根據題意可證△AOC∽△CDB.
∴![]() .
.
∴![]() .
.
∴m(5-m)=2.
∴m2-5m+2=0.
∴m是方程x2-5x+2=0的實數根.
(3)
解:方程ax2+bx+c=0(a≠0)可化為
x2+![]() x+
x+![]() =0.
=0.
模仿研究小組作法可得:A(0,1),B(-![]() ,
,![]() )或A(0,
)或A(0,![]() ),B(-
),B(-![]() ,c)等.
,c)等.
(4)
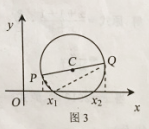
解:以圖3為例:P(m1,n1)Q(m2,n2),
設方程的根為x,根據三角形相似可得.![]() =
=![]() .
.
上式可化為x2-(m1+m2)x+m1m2+n1n2=0.
又ax2+bx+c=0,
即x2+![]() x+
x+![]() =0.
=0.
比較系數可得:m1+m2=-![]() .
.
m1m2+n1n2=![]() .
.
【解析】(1)根據題目中給的操作步驟操作即可得出圖2中的圖.
(2)在圖1中,過點B作BD⊥x軸,交x軸于點D.依題意可證△AOC∽△CDB.然后根據相似三角形對應邊的比相等列出式子,化簡后為m2-5m+2=0,從而得證。
(3)將方程ax2+bx+c=0(a≠0)可化為x2+![]() x+
x+![]() =0.模仿研究小組作法即可得答案。
=0.模仿研究小組作法即可得答案。
(4)以圖3為例:P(m1,n1)Q(m2,n2),設方程的根為x,根據三角形相似可得.![]() =
=![]() .化簡后為x2-(m1+m2)x+m1m2+n1n2=0.
.化簡后為x2-(m1+m2)x+m1m2+n1n2=0.
又x2+![]() x+
x+![]() =0.再依據相對應的系數相等即可求出。
=0.再依據相對應的系數相等即可求出。
【考點精析】利用根與系數的關系和相似三角形的判定與性質對題目進行判斷即可得到答案,需要熟知一元二次方程ax2+bx+c=0(a≠0)的根由方程的系數a、b、c而定;兩根之和等于方程的一次項系數除以二次項系數所得的商的相反數;兩根之積等于常數項除以二次項系數所得的商;相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方.


科目:初中數學 來源: 題型:
【題目】將下列各數填入相應的集合中.
—7 , 0, ![]() ,—22
,—22![]() , -2.55555…, 3.01, +9 ,4.020020002…,+10﹪, -2
, -2.55555…, 3.01, +9 ,4.020020002…,+10﹪, -2![]() .
.
無理數集合:{ }; 負有理數集合:{ };
正分數集合:{ }; 非負整數集合:{ };
查看答案和解析>>
科目:初中數學 來源: 題型:
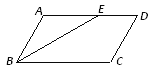
【題目】平行四邊形ABCD中,∠ABC的角平分線BE將邊AD分成長度為5cm和6cm的兩部分,則平行四邊形ABCD的周長為__________________cm.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示的運算程序中,若開始輸入的x值為100,我們發現第1次輸出的結果為50,第2次輸出的結果為25,…,第2018次輸出的結果為_________.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為做好食堂的服務工作,某學校食堂對學生最喜愛的菜肴進行了抽樣調查,下面試根據收集的數據繪制的統計圖(不完整):
(1)參加抽樣調查的學生數是______人,扇形統計圖中“大排”部分的圓心角是______°;
(2)把條形統計圖補充完整;
(3)若全校有3000名學生,請你根據以上數據估計最喜愛“烤腸”的學生人數.


查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某景區一電瓶小客車接到任務從景區大門出發,向東走2千米到達A景區,繼續向東走2.5千米到達B景區,然后又回頭向西走8.5千米到達C景區,最后回到景區大門.
![]()
(1)以景區大門為原點,向東為正方向,以1個單位長表示1千米,建立如圖所示的數軸,請在數軸上表示出上述A、B、C三個景區的位置.
(2)A景區與C景區之間的距離是多少?
(3)若電瓶車充足一次電能行走15千米,則該電瓶車能否在一開始充足電而途中不充電的情況下完成此次任務?請計算說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A,B,D的坐標為(1,0),(3,0),(0,1),點C在第四象限,∠ACB=90°,AC=BC.若△ABC與△A'B'C'關于點D成中心對稱,則點C'的坐標為______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】王紅有5張寫著以下數字的卡片,請按要求抽出卡片,完成下列各題:![]()
(1)從中取出2張卡片,使這2張卡片上數字乘積最小,最小值是 .
(2)從中取出2張卡片,使這2張卡片數字相除商最大,最大值是 .
(3)從中取出除0以外的4張卡片,將這4個數字進行加、減、乘、除或乘方等混合運算,使結果為24,(注:每個數字只能用一次,如:23×[1﹣(﹣2)]),請另寫出一種符合要求的運算式子 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將直角邊長為6的等腰直角△AOC放在平面直角坐標系中,點O為坐標原點,點C、A分別在x軸,y軸的正半軸上,一條拋物線經過點A、C及點B(﹣3,0).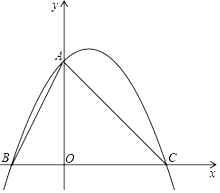
(1)求該拋物線的解析式;
(2)若點P是線段BC上一動點,過點P作AB的平行線交AC于點E,連接AP,當△APE的面積最大時,求點P的坐標;
(3)若點P(t,t)在拋物線上,則稱點P為拋物線的不動點,將(1)中的拋物線進行平移,平移后,該拋物線只有一個不動點,且頂點在直線y=2x﹣ ![]() 上,求此時拋物線的解析式.
上,求此時拋物線的解析式.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com