
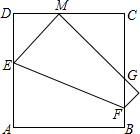
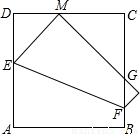
 小麗將一個邊長為2a的正方形紙片ABCD折疊,頂點A落到CD邊上的點M的位置,折痕交AD于E,交BC于F,邊AB折疊后與BC邊交于點G(如圖).在折疊過程中,小麗發現當點M在CD邊上的任意位置時,(點C,D除外),△CMG的周長總是相等的,那么△CMG的周長為________.
小麗將一個邊長為2a的正方形紙片ABCD折疊,頂點A落到CD邊上的點M的位置,折痕交AD于E,交BC于F,邊AB折疊后與BC邊交于點G(如圖).在折疊過程中,小麗發現當點M在CD邊上的任意位置時,(點C,D除外),△CMG的周長總是相等的,那么△CMG的周長為________.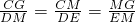 ,即
,即 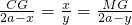
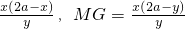
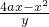
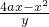 =
=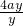 =4a.
=4a.

科目:初中數學 來源: 題型:
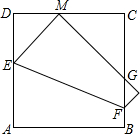 小麗將一個邊長為2a的正方形紙片ABCD折疊,頂點A落到CD邊上的點M的位置,折痕交AD于E,交BC于F,邊AB折疊后與BC邊交于點G(如圖).在折疊過程中,小麗發現當點M在CD邊上的任意位置時,(點C,D除外),△CMG的周長總是相等的,那么△CMG的周長為
小麗將一個邊長為2a的正方形紙片ABCD折疊,頂點A落到CD邊上的點M的位置,折痕交AD于E,交BC于F,邊AB折疊后與BC邊交于點G(如圖).在折疊過程中,小麗發現當點M在CD邊上的任意位置時,(點C,D除外),△CMG的周長總是相等的,那么△CMG的周長為查看答案和解析>>
科目:初中數學 來源:2007年第5屆“學用杯”全國數學知識應用競賽九年級初賽試卷(解析版) 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com