
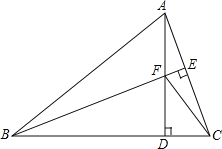
【題目】如圖,在△ABC中,AB=BC,BE⊥AC于點E,AD⊥BC于點D,∠BAD=45°,CD=![]() ,AD與BE交于點F,連接CF,則AD的長為_____.
,AD與BE交于點F,連接CF,則AD的長為_____.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
【題目】為鼓勵大學畢業生自主創業,某市政府出臺了相關政策:由政府協調,本市企業按成本價提供產品給大學畢業生自主銷售,成本價與出廠價之間的差價由政府承擔.李明按照相關政策投資銷售本市生產的一種新型節能燈.已知這種節能燈的成本價為每件8元,出廠價為每件10元,每月銷售量y(件)與銷售單價x(元)之間的關系近似滿足一次函數:y=-10x+500.
(1)李明在開始創業的第一個月將銷售單價定為20元,那么政府這個月為他承擔的總差價為多少元?
(2)設李明獲得的利潤為w(元),當銷售單價定為多少元時,每月可獲得最大利潤?
(3)物價部門規定,這種節能燈的銷售單價不得高于25元.如果李明想要每月獲得的利潤不低于3410元,那么政府為他承擔的總差價最少為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】深圳某百果園店售賣贛南臍橙,已知每千克臍橙的成本價為![]() 元,在銷售臍橙的這
元,在銷售臍橙的這![]() 天時間內,銷售單價
天時間內,銷售單價![]() (元/千克)與時間第
(元/千克)與時間第![]() (天)之間的函數關系式為
(天)之間的函數關系式為![]() (
(![]() ,且
,且![]() 為整數),日銷售量
為整數),日銷售量![]() (千克)與時間第
(千克)與時間第![]() (天)之間的函數關系式為
(天)之間的函數關系式為![]() (
(![]() ,且
,且![]() 為整數)
為整數)
(1)請你直接寫出日銷售利潤![]() (元)與時間第
(元)與時間第![]() (天)之間的函數關系式;
(天)之間的函數關系式;
(2)該店有多少天日銷售利潤不低于![]() 元?
元?
(3)在實際銷售中,該店決定每銷售![]() 千克臍橙,就捐贈
千克臍橙,就捐贈![]() 元給希望工程,在這
元給希望工程,在這![]() 天中,每天扣除捐贈后的日銷售利潤隨時間
天中,每天扣除捐贈后的日銷售利潤隨時間![]() 的增大而增大,求
的增大而增大,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在完善基礎設施、改善市容市貌、提升城市品質過程中,2019年我市開展人行道改造工程,需要花崗巖地板磚鋪設人行道.現租用甲、乙兩種貨車運載地板磚,已知一輛甲車每次運載的重量比一輛乙車多2噸,且甲車運載16噸地板磚和乙車運載12噸地板磚所用的車輛數相同.
(1)甲、乙兩種貨車每次運載地板磚各多少噸?
(2)現租用甲車a輛、乙車b輛,剛好運載地板磚100噸,且a≤3b,共有多少種租車方案?
(3)在(2)中已知一輛甲車每次的運費是380元,一輛乙車每次的運費是300元,如何租用甲、乙兩種車可使得總運費最低?求出最低總運費.
查看答案和解析>>
科目:初中數學 來源: 題型:
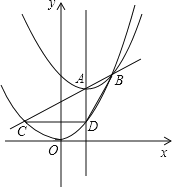
【題目】如圖,在平面直角坐標系中,一次函數y=![]() x﹣2的圖象分別交x、y軸于點A、B,拋物線y=x2+bx+c經過點A、B,點P為第四象限內拋物線上的一個動點.
x﹣2的圖象分別交x、y軸于點A、B,拋物線y=x2+bx+c經過點A、B,點P為第四象限內拋物線上的一個動點.
(1)求此拋物線的函數解析式;
(2)過點P作PM∥y軸,分別交直線AB、x軸于點C、D,若以點P、B、C為頂點的三角形與以點A、C、D為頂點的三角形相似,求點P的坐標;
(3)當∠PBA=2∠OAB時,求點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】A是直線x=1上一個動點,以A為頂點的拋物線y1=a(x﹣1)2+t和拋物線y2=ax2交于點B(A,B不重合,a是常數),直線AB和拋物線y2=ax2交于點B,C,直線x=1和拋物線y2=ax2交于點D.(如圖僅供參考)
(1)求點B的坐標(用含有a,t的式子表示);
(2)若a<0,且點A向上移動時,點B也向上移動,求![]() 的范圍;
的范圍;
(3)當B,C重合時,求![]() 的值;
的值;
(4)當a>0,且△BCD的面積恰好為3a時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】問題情境:
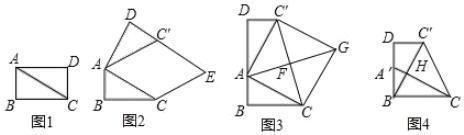
在綜合與實踐課上,老師讓同學們以“矩形紙片的剪拼”為主題開展數學活動.如 圖 1,將:矩形紙片 ABCD 沿對角線 AC 剪開,得到△ABC 和△ACD.并且量得 AB =4cm,AC=8cm.
操作發現:
(1)將圖 1 中的△ACD 以點 A 為旋轉中心,按逆時針方向旋轉∠α,使∠α=∠BAC,得到如圖 2 所示的△AC′D,過點 C 作 AC′的平行線,與 DC'的延長線 交于點 E,則四邊形 ACEC′的形狀是 .
(2)創新小組將圖 1 中的△ACD 以點 A 為旋轉中心,按逆時針方向旋轉,使 B、 A、D 三點在同一條直線上,得到如圖 3 所示的△AC′D,連接 CC',取 CC′的中 點 F,連接 AF 并延長至點 G,使 FG=AF,連接 CG、C′G,得到四邊形 ACGC′, 發現它是正方形,請你證明這個結論.
實踐探究:
(3)縝密小組在創新小組發現結論的基礎上,進行如下操作:將△ABC 沿著 BD 方向平移,使點 B 與點 A 重合,此時 A 點平移至 A'點,A'C 與 BC′相交于點 H, 如圖 4 所示,連接 CC′,試求 tan∠C′CH 的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y=mx2+(1﹣2m)x+1﹣3m.
(1)當m=2時,求二次函數圖象的頂點坐標;
(2)已知拋物線與x軸交于不同的點A、B.
①求m的取值范圍;
②若3≤m≤4時,求線段AB的最大值及此時二次函數的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
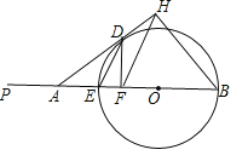
【題目】已知,如圖,EB是![]() 的直徑,且
的直徑,且![]() ,在BE的延長線上取點P,使
,在BE的延長線上取點P,使![]() ,A是EP上一點,過A作
,A是EP上一點,過A作![]() 的切線,切點為D,過D作
的切線,切點為D,過D作![]() 于F,過B作AD的垂線BH,交AD的延長線于
于F,過B作AD的垂線BH,交AD的延長線于![]() 當點A在EP上運動,不與E重合時:
當點A在EP上運動,不與E重合時:
![]() 是否總有
是否總有![]() ,試證明你的結論;
,試證明你的結論;
![]() 設
設![]() ,
,![]() ,求y和x的函數關系,并寫出x的取值范圍.
,求y和x的函數關系,并寫出x的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com