
【題目】閱讀下面材料
在數軸上4與![]() 所對的兩點之間的距離:
所對的兩點之間的距離:![]()
在數軸上![]() 與3所對的兩點之間的距離
與3所對的兩點之間的距離![]() ;
;
在數軸上![]() 與
與![]() 所對的兩點之間的距離:
所對的兩點之間的距離:![]() 在數軸上點A、B分別表示數a、b,則A、B兩點之間的距離
在數軸上點A、B分別表示數a、b,則A、B兩點之間的距離![]()
依據材料知識解答下列問題
![]() 數軸上表示
數軸上表示![]() 和
和![]() 的兩點之間的距離是______,數軸上表示數x和3的兩點之間的距離表示為______;
的兩點之間的距離是______,數軸上表示數x和3的兩點之間的距離表示為______;
![]() 七年級研究性學習小組進行如下探究:
七年級研究性學習小組進行如下探究:
![]() 請你在草稿紙上面出數軸當表示數x的點在
請你在草稿紙上面出數軸當表示數x的點在![]() 與2之間移動時,
與2之間移動時,![]() 的值總是一個固定的值為:______,式子
的值總是一個固定的值為:______,式子![]() 的最小值是______.
的最小值是______.
![]() 請你在草稿紙上畫出數軸,當x等于______時,
請你在草稿紙上畫出數軸,當x等于______時,![]() 的值最小,且最小值是______.
的值最小,且最小值是______.
【答案】(1)2,![]() 或
或![]() (2)①5,1②2,7
(2)①5,1②2,7
【解析】
![]() 根據數軸上A、B兩點之間的距離
根據數軸上A、B兩點之間的距離![]() 的表達式計算出絕對值;
的表達式計算出絕對值;
![]() 要去掉絕對值符號,需要抓住已知點在數軸上進行分段討論,寫出去絕對值后的表達式討論計算即可.
要去掉絕對值符號,需要抓住已知點在數軸上進行分段討論,寫出去絕對值后的表達式討論計算即可.
![]() 根據題意知
根據題意知![]() 和
和![]() 的兩點之間的距離可表示為:
的兩點之間的距離可表示為:![]() ;數x和3的兩點之間的距離
;數x和3的兩點之間的距離![]() 或
或![]() ;
;
故答案為2,![]() 或
或![]() ;
;
![]()
![]() ,
,
![]() ,
,![]() ,
,
![]()
所以當![]() 時,
時,![]() 的值總是一個固定的值為5.
的值總是一個固定的值為5.
![]() 是表示x到A、C的距離之和,可觀察下圖.
是表示x到A、C的距離之和,可觀察下圖.
當![]() 時,由
時,由![]() 可知
可知![]()
當![]() 時,
時,![]()
![]() 當
當![]() 時,式子
時,式子![]() 的最小值是1.
的最小值是1.
故答案為5,1.
![]() 畫出圖形,則可知,
畫出圖形,則可知,![]() 是表示x的點到A、B、C三點距離之和
是表示x的點到A、B、C三點距離之和
分區間來討論,可以得出
當![]() 時,
時,![]() ,可見
,可見![]() 取得最小值,
取得最小值,![]() ;
;
當![]() 時,
時,![]() ,
,![]() 時取得最小值,
時取得最小值,![]() .
.
所以式![]() 當x等于2時,最小值是7.
當x等于2時,最小值是7.
故答案為2,7.


 陽光試卷單元測試卷系列答案
陽光試卷單元測試卷系列答案科目:初中數學 來源: 題型:
【題目】小東家與學校之間是一條筆直的公路,早飯后,小東歩行前往學校,途中發現忘帶畫板,停下給媽媽打電話,媽媽接到電話后,帶上畫板馬上趕往學校,同時小東沿原路返回,兩人相遇后,小東立即趕往學校,媽媽沿原路返回,![]() 時到家,假設小東始終以
時到家,假設小東始終以![]() 的速度步行,兩人離家的距離
的速度步行,兩人離家的距離![]() (單位:
(單位:![]() )與小東打完電話后的步行時間
)與小東打完電話后的步行時間![]() (單位:
(單位:![]() )之間的函數關系如圖所示:
)之間的函數關系如圖所示:

(1)小東打電話時,他離家__________![]() .
.
(2)在圖中的空格中,填上相應的數據.
(3)小東和媽媽相遇后,媽媽回家的速度為_________![]() .
.
(4)_____________ ![]() 時,兩人相距
時,兩人相距![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠準備用圖甲所示的![]() 型正方形板材和
型正方形板材和![]() 型長方形板材,制作成圖乙所示的豎式和橫式兩種無蓋箱子.
型長方形板材,制作成圖乙所示的豎式和橫式兩種無蓋箱子.
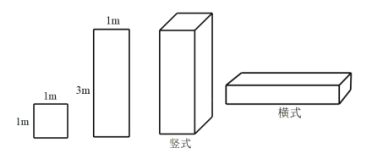
(1)若該工廠準備用不超過2400元的資金去購買![]() ,
,![]() 兩種型號板材,制作豎式、橫式箱子共10個,已知
兩種型號板材,制作豎式、橫式箱子共10個,已知![]() 型板材每張20元,
型板材每張20元,![]() 型板材每張60元,問最多可以制作豎式箱子多少只?
型板材每張60元,問最多可以制作豎式箱子多少只?
(2)若該工程新購得65張規格為![]() 型正方形板材,將其全部切割測好難過
型正方形板材,將其全部切割測好難過![]() 型或
型或![]() 型板材(不計損耗),用切割的板材制作兩種類型的箱子,要求豎式箱子不少于10只,且材料恰好用完,則能制作豎式箱子______只.
型板材(不計損耗),用切割的板材制作兩種類型的箱子,要求豎式箱子不少于10只,且材料恰好用完,則能制作豎式箱子______只.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,EF過平行四邊形ABCD對角線的交點O,交AD于E,交BC于F,若平行四邊形ABCD的周長為18,OE=1.5,則四邊形EFCD的周長為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明某天上午9時騎自行車離開家,15時回家,他離家的距離與時間的變化情況如圖所示.

(1)10時時他離家 ![]() ,他到達離家最遠的地方時是 時,此時離家
,他到達離家最遠的地方時是 時,此時離家 ![]() ;
;
(2)他可能在哪段時間內休息,并吃午餐?
(3)他在出行途中,哪段時間內騎車速度最快,速度是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在下列四項調查中,方式正確的是![]()
![]()
A. 了解本市中學生每天學習所用的時間,采用全面調查的方式
B. 為保證運載火箭的成功發射,對其所有的零部件采用抽樣調查的方式
C. 了解某市每天的流動人口數,采用全面調查的方式
D. 了解全市中學生的視力情況,采用抽樣調查的方式
查看答案和解析>>
科目:初中數學 來源: 題型:
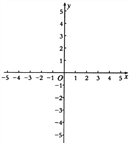
【題目】已知二次函數![]() .
.
(1)證明:不論![]() 取何值,該函數圖像與
取何值,該函數圖像與![]() 軸總有公共點;
軸總有公共點;
(2)若該函數的圖像與![]() 軸交于點(0,3),求出頂點坐標并畫出該函數圖像;
軸交于點(0,3),求出頂點坐標并畫出該函數圖像;
(3)在(2)的條件下,觀察圖像,解答下列問題:
①不等式![]() 的的解集是 ;
的的解集是 ;
②若一元二次方程![]() 有兩個不相等的實數根,則
有兩個不相等的實數根,則![]() 的取值范圍是 ;
的取值范圍是 ;
③若一元二次方程![]() 在
在![]() 的范圍內有實數根,則
的范圍內有實數根,則![]() 的取
的取
值范圍是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠現有甲種原料3600kg,乙種原料2410kg,計劃利用這兩種原料生產A,B兩種產品共500件,產品每月均能全部售出.已知生產一件A產品需要甲原料9kg和乙原料3kg;生產一件B種產品需甲種原料4kg和乙種原料8kg.
(1)設生產x件A種產品,寫出x應滿足的不等式組.
(2)問一共有幾種符合要求的生產方案?并列舉出來.
(3)若有兩種銷售定價方案,第一種定價方案可使A產品每件獲得利潤1.15萬元,B產品每件獲得利潤1.25萬元;第二種定價方案可使A和B產品每件都獲得利潤1.2萬元;在上述生產方案中哪種定價方案盈利最多?(請用數據說明)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,學校大門出口處有一自動感應欄桿,點A是欄桿轉動的支點,當車輛經過時,欄桿AE會自動升起,某天早上,欄桿發生故障,在某個位置突然卡住,這時測得欄桿升起的角度∠BAE=127°,已知AB⊥BC,支架AB高1.2米,大門打開的寬度BC為2米,以下哪輛車可以通過?(欄桿寬度,汽車反光鏡忽略不計)(參考數據:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75.車輛尺寸:長×寬×高)( )
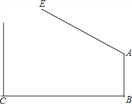
A. 寶馬Z4(4200mm×1800mm×1360mm) B. 奔馳smart(4000mm×1600mm×1520mm)
C. 大眾朗逸(4600mm×1700mm×1400mm) D. 奧迪A6L(4700mm×1800mm×1400mm)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com