国产高清亚洲,国产精品久久久久久久天堂,欧美一级一区

精英家教網(wǎng) > 初中數(shù)學 > 題目詳情

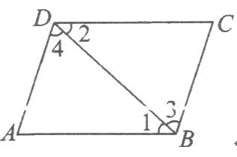
在括號內(nèi)填寫推理的依據(jù)，已知：如圖，AB∥CD，∠ABC=∠ADC，求證：AD∥BC.

證明：∵AB∥CD(____________)，∴∠1= ____________ ( ____________ ).

又∵∠ABC=∠ADC ( ____________ )，∴∠ABC-∠1=∠ADC-∠2.

即∠3=∠4，∴AD∥____________ ( ____________ ).

答案：已知 ∠2 兩直線平行，內(nèi)錯角相等

已知

BC 內(nèi)錯角相等 ,兩直線平行

練習冊系列答案

1加1閱讀好卷系列答案

專項復(fù)習訓(xùn)練系列答案

年級	高中課程	年級	初中課程
高一	高一免費課程推薦！	初一	初一免費課程推薦！
高二	高二免費課程推薦！	初二	初二免費課程推薦！
高三	高三免費課程推薦！	初三	初三免費課程推薦！
更多初中、高中輔導(dǎo)課程推薦,點擊進入>>

相關(guān)習題

科目：初中數(shù)學 來源： 題型：

29、如圖，已知點D、E為△ABC的邊BC上兩點．AD=AE，BD=CE，為了判斷∠B與∠C的大小關(guān)系，請你填空完成下面的推理過程，并在空白括號內(nèi)注明推理的依據(jù)．
解：過點A作AH⊥BC，垂足為H．
∵在△ADE中，AD=AE（已知）
AH⊥BC（所作）
∴DH=EH（等腰三角形底邊上的高也是底邊上的中線）
又∵BD=CE（已知）
∴BD+DH=CE+EH（等式的性質(zhì)）
即：BH=

又∵

AH⊥BC

（所作）
∴AH為線段

的垂直平分線
∴AB=AC（線段垂直平分線上的點到線段兩個端點的距離相等）
∴

∠B=∠C

（等邊對等角）

查看答案和解析>>

科目：初中數(shù)學 來源： 題型：

已知：DC∥AB，DF平分∠CDB，BE平分∠ABD
求證：BE∥DF．在空格處填角括號內(nèi)填推理的依據(jù)
證明：∵DC∥AB（已知）
∴∠ABD=

∠CDB

（

兩直線平行，內(nèi)錯角相等

）
又∵DF平分∠CDB，BE平分∠ABD （已知）
∴∠1=

∠CBD

，∠2=

∠ABD

∴∠1=∠2（

等量代換

）
∴BE∥DF（

內(nèi)錯角相等，兩直線平行

）．

查看答案和解析>>

科目：初中數(shù)學 來源： 題型：

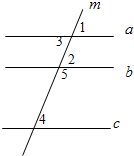在橫線上填上結(jié)論并在括號內(nèi)填寫相應(yīng)的理由
已知：如圖，∠1=∠2，∠3=∠4，則運用所學知識推理如下：
推理①∵∠1=∠2（已知）
∴

∥

（

同位角相等，兩直線平行

）
推理②又∵∠3=∠4（已知）
∴

∥

（

內(nèi)錯角相等，兩直線平行

）
推理③∵a∥b，a∥c（已證）
∴

∥

（

平行于同一條直線的兩直線平行

）
推理④∵c∥b（已證）
∴∠4+∠5=

180°

（

兩直線平行，同旁內(nèi)角互補

）

查看答案和解析>>

科目：初中數(shù)學 來源：2010年安慶市外國語學校八年級第一學期期中考試數(shù)學卷 題型：解答題

已知：DC∥AB DF平分∠CDB ，BE平分∠ABD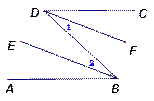

求證 BE∥DF    在空格處填角括號內(nèi)填推理的依據(jù)
證明 ∵DC∥AB（已知）
∴∠ABD=
（                                  ）
又∵DF平分∠CDB   BE平分∠ABD （已知）
∴∠1=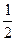            ∠2=        （                                 ）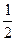
∴∠1=∠2  （          ）
∴BE∥DF    （                                      ）

查看答案和解析>>

同步練習冊答案

日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

練習冊

高中

初中

小學