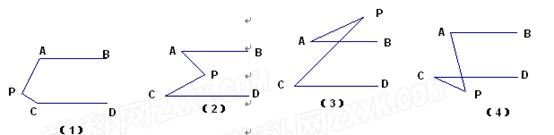
日日人人_亚洲美女在线视频_av手机在线播放_国产大片aaa_欧美中文日韩_午夜理伦三级

精英家教網 > 初中數學 > 題目詳情

探究（共8分）

已知，ＡＢ∥ＣＤ，分別探討四個圖形中∠ＡＰＣ，∠ＰＡＢ，∠ＰＣＤ的關系.

(1)請探究圖1、圖2中三個角的關系，并任選一個加以證明.

(2)猜想圖3、圖4中三個角的關系，不必說明理由. （提示：注意適當添加輔助線吆！）

 

【答案】

略

【解析】略

 

練習冊系列答案
相關習題

科目：初中數學 來源： 題型：閱讀理解

（2012•李滄區一模）【問題引入】
幾個人拎著水桶在一個水龍頭前面排隊打水，水桶有大有小．他們該怎樣排隊才能使得總的排隊時間最短？
假設只有兩個人時，設大桶接滿水需要T分鐘，小桶接滿水需要t分鐘（顯然T＞t），若拎著大桶者在拎著小桶者之前，則拎大桶者可直接接水，只需等候T分鐘，拎小桶者一共等候了（T+t）分鐘，兩人一共等候了（2T+t）分鐘；反之，若拎小桶者在拎大桶者前面，容易求出出兩人接滿水等候（T+2t）分鐘．可見，要使總的排隊時間最短，拎小桶者應排在拎大桶者前面．這樣，我們可以猜測，幾個人拎著水桶在一個水龍頭前面排隊打水，要使總的排隊時間最短，需將他們按水桶從小到大排隊．
規律總結：
事實上，只要不按從小到大的順序排隊，就至少有緊挨著的兩個人拎著大桶者排在拎小桶者之前，仍設大桶接滿水需要T分鐘，小桶接滿水需要t分鐘，并設拎大桶者開始接水時已等候了m分鐘，這樣拎大桶者接滿水一共等候了（m+T）分鐘，拎小桶者一共等候了（m+T+t）分鐘，兩人一共等候了（2m+2T+t）分鐘，在其他人位置不變的前提下，讓這兩個人交還位置，即局部調整這兩個人的位置，同樣介意計算兩個人接滿水共等候了
2m+2t+T
2m+2t+T
分鐘，共節省了
T-t
T-t
分鐘，而其他人等候的時間未變，這說明只要存在有緊挨著的兩個人是拎大桶者在拎小桶者之前都可以這樣調整，從而使得總等候時間減少．這樣經過一系列調整后，整個隊伍都是從小打到排列，就打到最優狀態，總的排隊時間就最短．
【方法探究】
一般的，對某些設計多個可變對象的數學問題，先對其少數對象進行調整，其他對象暫時保持不變，從而化難為易，取得問題的局部解決．經過若干次這種局部的調整，不斷縮小范圍，逐步逼近目標，最終使問題得到解決，這種數學思想就叫做局部調整法．
【實踐應用1】
如圖1在銳角△ABC中，AB=4
2
，∠BAC=45°，∠BAC的平分線交BC于點D，M、N分別是AD和AB上的動點，則BM+MN的最小值是多少？
解析：
（1）先假定N為定點，調整M到合適的位置使BM+MN有最小值（相對的），容易想到，在AC上作AN′=AN（即作點N關于AD的對稱點N'），連接BN′交AD于M，則M點是使BM+MN有相對最小值的點．（如圖2，M點是確定方法找到的）
（2）在考慮點N的位置，使BM+MN最終達到最小值．可以理解，BM+MN=BM+MN′，所以要使BM+MN′有最小值，只需使
BM+MN′=BN′
BM+MN′=BN′
，此時BM+MN的最小值是
4
4
．
【實踐應用2】
如圖3，把邊長是3的正方形等分成9個小正方形，在有陰影的小正方形內（包括邊界）分別取點P、R，于已知格點Q（每個小正方形的頂點叫做格點）構成三角形，則△PQR的最大面積是
2
2
，請在圖4中畫出面積最大時的△PQR的圖形．

查看答案和解析>>

科目：初中數學 來源： 題型：

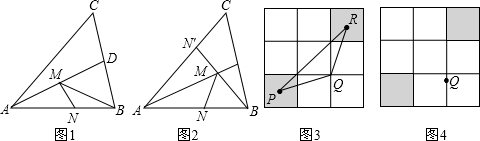
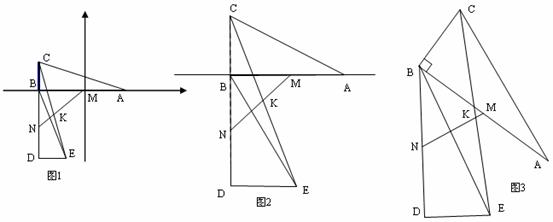
在直角坐標系中，∠ABC=∠BDE=90°，BC=DE，AC=BE，M、N分別是AB、BD的中點，連接MN交CE于點K.

(1)如圖1,已知A點的坐標為(3,0),C點的坐標為(-4,2),求D點的坐標.

(2)如圖2當C、B、D共線,AB=2BC時,探究CK與EK之間的數量關系,并證明.

(3)如圖3當C、B、D不共線,AB≠BC時,(2)中的結論是否成立,若成立,請證明;若不成立,請說明理由.

查看答案和解析>>

科目：初中數學 來源：2012年山東省青島市李滄區中考數學一模試卷（解析版） 題型：解答題

【問題引入】
幾個人拎著水桶在一個水龍頭前面排隊打水，水桶有大有小．他們該怎樣排隊才能使得總的排隊時間最短？
假設只有兩個人時，設大桶接滿水需要T分鐘，小桶接滿水需要t分鐘（顯然T＞t），若拎著大桶者在拎著小桶者之前，則拎大桶者可直接接水，只需等候T分鐘，拎小桶者一共等候了（T+t）分鐘，兩人一共等候了（2T+t）分鐘；反之，若拎小桶者在拎大桶者前面，容易求出出兩人接滿水等候（T+2t）分鐘．可見，要使總的排隊時間最短，拎小桶者應排在拎大桶者前面．這樣，我們可以猜測，幾個人拎著水桶在一個水龍頭前面排隊打水，要使總的排隊時間最短，需將他們按水桶從小到大排隊．
規律總結：
事實上，只要不按從小到大的順序排隊，就至少有緊挨著的兩個人拎著大桶者排在拎小桶者之前，仍設大桶接滿水需要T分鐘，小桶接滿水需要t分鐘，并設拎大桶者開始接水時已等候了m分鐘，這樣拎大桶者接滿水一共等候了（m+T）分鐘，拎小桶者一共等候了（m+T+t）分鐘，兩人一共等候了（2m+2T+t）分鐘，在其他人位置不變的前提下，讓這兩個人交還位置，即局部調整這兩個人的位置，同樣介意計算兩個人接滿水共等候了______分鐘，共節省了______分鐘，而其他人等候的時間未變，這說明只要存在有緊挨著的兩個人是拎大桶者在拎小桶者之前都可以這樣調整，從而使得總等候時間減少．這樣經過一系列調整后，整個隊伍都是從小打到排列，就打到最優狀態，總的排隊時間就最短．
【方法探究】
一般的，對某些設計多個可變對象的數學問題，先對其少數對象進行調整，其他對象暫時保持不變，從而化難為易，取得問題的局部解決．經過若干次這種局部的調整，不斷縮小范圍，逐步逼近目標，最終使問題得到解決，這種數學思想就叫做局部調整法．
【實踐應用1】
如圖1在銳角△ABC中，AB=，∠BAC=45°，∠BAC的平分線交BC于點D，M、N分別是AD和AB上的動點，則BM+MN的最小值是多少？
解析：
（1）先假定N為定點，調整M到合適的位置使BM+MN有最小值（相對的），容易想到，在AC上作AN′=AN（即作點N關于AD的對稱點N'），連接BN′交AD于M，則M點是使BM+MN有相對最小值的點．（如圖2，M點是確定方法找到的）
（2）在考慮點N的位置，使BM+MN最終達到最小值．可以理解，BM+MN=BM+MN′，所以要使BM+MN′有最小值，只需使______，此時BM+MN的最小值是______．
【實踐應用2】
如圖3，把邊長是3的正方形等分成9個小正方形，在有陰影的小正方形內（包括邊界）分別取點P、R，于已知格點Q（每個小正方形的頂點叫做格點）構成三角形，則△PQR的最大面積是______，請在圖4中畫出面積最大時的△PQR的圖形．

查看答案和解析>>

科目：初中數學 來源： 題型：

探究（共8分）

已知，ＡＢ∥ＣＤ，分別探討四個圖形中∠ＡＰＣ，∠ＰＡＢ，∠ＰＣＤ的關系.

(1)請探究圖1、圖2中三個角的關系，并任選一個加以證明.

(2)猜想圖3、圖4中三個角的關系，不必說明理由. （提示：注意適當添加輔助線吆！）

 

查看答案和解析>>

同步練習冊答案
主站蜘蛛池模板： 欧美日韩一区二区三区在线观看 | 国产成人精品一区一区一区 | 国产日韩中文字幕 | 一区二区三区在线播放视频 | 色婷婷综合网 | 一区二区三区免费看 | 天堂一区二区三区 | 国产一区二区三区久久久久久 | 日本黄区免费视频观看 | 国产成人涩涩涩视频在线观看 | 成人二区 | 日韩城人免费 | 伊人网站在线 | 四虎影视精品 | 香蕉黄色一级片 | 国产剧情一区二区 | 国产精品久久久久蜜臀 | 国产成人激情 | 成人二区 | 久久久久国产视频 | 久热最新 | 欧美电影一区二区三区 | 操久久 | 亚洲自拍一区在线 | 免费99精品国产自在在线 | 亚洲免费小视频 | 亚洲成人免费网址 | 日本一区二区高清视频 | 精品国产乱码久久久久久影片 | 久久久久久久久一区二区 | 免费观看视频www | 伊人爽| 中文字幕欧美在线观看 | 国产福利一区二区三区四区 | 精品一区二区三区久久久 | 黄色免费网站 | 成人av影片在线观看 | 亚洲免费视频大全 | avhd101在线成人播放 | 美女131mm久久爽爽免费 | 欧美在线视频不卡 |