
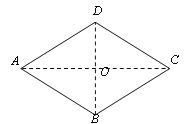
【題目】已知:如圖,四邊形ABCD是菱形,AB=AD.
求證:(1) AB=BC=CD=DA
(2) AC⊥DB
(3) ∠ADB=∠CDB,∠ABD=∠CBD,∠DAC=∠BAC,∠DCA=∠BCA
【答案】(1)證明見解析;(2)證明見解析;(3)證明見解析.
【解析】
(1)根據菱形定義:一組鄰邊相等的平行四邊形是菱形即可解答;(2)利用SSS證明△ADO≌△CDO,可得:∠AOD=∠COD,又因為∠AOD+∠COD=180°,所以∠AOD=∠COD=90°即可得出AC⊥DB;(3)由△ADO≌△CDO,再根據全等三角形對應角相等,兩直線平行,內錯角相等即可解答.
證明:(1)∵四邊形ABCD是菱形,∴AB=CD,AD=CB.
又∵AB=AD,∴AB=BC=CD=DA.
(2)在△ADO和△CDO中,
∵DA=DC,DO=DO,AO=CO,∴△ADO≌△CDO. ∴∠AOD=∠COD.
∵∠AOD+∠COD=180°,∴∠AOD=∠COD=90°. ∴AC⊥DB.
(3) ∵△ADO≌△CDO, ∴∠ADB=∠CDB,∠DAC=∠DCA.
∵AB∥CD,AD∥CB,
∴∠ADB=∠CBD,∠CDB=∠ABD,∠DAC=∠BCA,∠DCA=∠BAC.
∴∠ADB=∠CDB,∠ABD=∠CBD,∠DAC=∠BAC,∠DCA=∠BCA.


 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ACB=90°,點E,F在邊AB上,將邊AC沿CE翻折,使點A落在AB上的點D處,再將邊BC沿CF翻折,使點B落在CD的延長線上的點B'處.

(1)求∠ECF的度數;
(2)若CE=4,B'F=1,求線段BC的長和△ABC的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠AOB,以O為圓心,以任意長為半徑作弧,分別交OA,OB于F,E兩點,再分別以E,F為圓心,大于![]() EF長為半徑作圓弧,兩條圓弧交于點P,作射線OP,過點F作FD∥OB交OP于點D.
EF長為半徑作圓弧,兩條圓弧交于點P,作射線OP,過點F作FD∥OB交OP于點D.
(1)若∠OFD=116°,求∠DOB的度數;
(2)若FM⊥OD,垂足為M,求證:△FMO≌△FMD.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() 、
、![]() 分別是
分別是![]() 、
、![]() 軸上兩點,其中
軸上兩點,其中![]() 與
與![]() 互為相反數.點
互為相反數.點![]() 是第二象限內一點,且
是第二象限內一點,且![]() ,點
,點![]() 是直線
是直線![]() 上一動點;
上一動點;
(1)若![]() ,且
,且![]() 是等腰三角形,求
是等腰三角形,求![]() 的度數;
的度數;
(2)點![]() 在直線
在直線![]() 上運動過程中,當
上運動過程中,當![]() 最短時,求
最短時,求![]() 的大小.
的大小.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知長方形ABCD的兩個頂點A(2,﹣1),C(6,2),點M為y軸上一點,△MAB的面積為6.請解答下列問題:
(1)頂點B的坐標 ;
(2)連接BD,求BD的長;
(3)請直接寫出點M的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
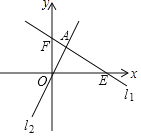
【題目】如圖,在平面直角坐標系中,點E的坐標為(4,0),點F的坐標為(0,2),直線11經過點E和點F,直線l1與直線l2:y=2x相交于點A.
(1)求直線l1的表達式;
(2)求點A的坐標;
(3)求△AOE的面積;
(4)當點P是直線l1上的一個動點時,過點P作y軸的平行線PB交直線l2于點B,當線段PB=3時,請直接寫出P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列分式方程解應用題
“互聯網+”已經成為我們生活中不可或缺的一部分,例如OFO.摩拜等互聯網共享單車就為城市短距離出行難提俱了解決方案,小明每天乘坐公交汽車上學,他家與公交站臺相距1.2km,現在每天租用共享單車到公交站臺所花時間比過去步行少12min,已知小明騎自行車的平均速度是步行平均速度的2.5倍,求小明步行的平均速度是多少km/h?
查看答案和解析>>
科目:初中數學 來源: 題型:
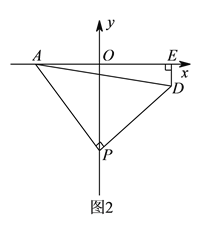
【題目】如圖![]() ,
, ![]() ,
, ![]() ,以
,以![]() 點為頂點、
點為頂點、![]() 為腰在第三象限作等腰
為腰在第三象限作等腰![]() .
.
(![]() )求
)求![]() 點的坐標.
點的坐標.
(![]() )如圖
)如圖![]() ,
, ![]() 為
為![]() 軸負半軸上一個動點,當
軸負半軸上一個動點,當![]() 點沿
點沿![]() 軸負半軸向下運動時,以
軸負半軸向下運動時,以![]() 為頂點,
為頂點, ![]() 為腰作等腰
為腰作等腰![]() ,過
,過![]() 作
作![]() 軸于
軸于![]() 點,求
點,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com